Курсовая работа: Графы и их представление на ЭВМ

Если v₀ = v_k , то маршрут замкнут, иначе открыт. Если все ребра различны, то маршрут называется цепью. Если все вершины (а значит, и ребра) различны, то маршрут называется простой цепью. В цепи v₀ , e₁ , v₁ , e₂ , v₂ ,…,e_k , v_k ,

вершины v₀ и v_k ,называются концами цепи. Говорят, что цепь с концами и и v соединяет вершины и и v . Цепь, соединяющая вершины и и v , обозначается (и, v ). Очевидно, что если есть цепь, соединяющая вершины и и v , то есть и простая цепь, соединяющая эти вершины.

Замкнутая цепь называется циклом; замкнутая простая цепь называется простым циклом. Число циклов в графе G обозначается z ( G ). Граф без циклов называется ациклическим.

Элементы графа – любое чередование вершин и рёбер графа, в котором каждому ребру предшествует смежная ей вершина, называющаяся контуром графа.

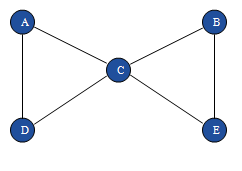
Рис 3.1 Маршруты, цепи, циклы

По рисунку 3.1 можно определить следующие утверждения:

1. A, C, A, D– маршрут, но не цепь;

2. A, C, E, B, C, D– цепь, но не простая цепь;

3. A, D, C, B, E, - простая цепь;

4. A, C, E, B, C, D, A– цикл, но не простой цикл;

5. A, C, D– простой цикл;

Цепь в ориентированном графе называется путём, а цикл – контуром.

3.2 Изоморфизм графов

Говорят, что два графа G ₁ ( V ₁ , Е₁ ) и G ₂ ( V ₂ , Е₂ ) изоморфны (обозначается G ₁ ~ G ₂ ), если существует биекция h : V ₁ ® V ₂ , сохраняющая смежность:

e₁ = ( u , v ) Î E₁ Þ e₂ = ( h( u ), h( v ) ) Î E₂ ,

e₂ = ( u , v ) Î E₂ Þ e₁ = ( h^-1 ( u ), h^-1 ( v ) ) Î E₁

Изоморфизм графов есть отношение эквивалентности. Действительно, изомор физм обладает всеми необходимыми свойствами:

1.рефлексивность: G ~ G , где требуемая биекция суть тождественная функция;

2.симметричность: если G ₁ ~ G ₂ с биекцией h, то G ₂ ~ G ₁ с биекцией h^-1 ;

3.транзитивность: если G ₁ ~ G ₂ с биекцией h, и G ₂ ~ G ₃ с биекцией g, тоG ₁ ~ G ₃ с биекцией goh.

Графы рассматриваются с точностью до изоморфизма, то есть рассматриваются классы эквивалентности по отношению изоморфизма.

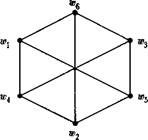Приведём примеры изоморфных графов рис. 3.2

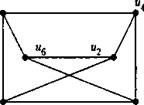
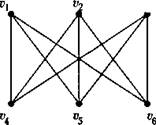
Рис. 3.2 Диаграммы изоморфных граф

Числовая характеристика, одинаковая для всех изоморфных графов, называется инвариантом графа. Так, р( G ) и д( G ) — инварианты графа С.

Не известно никакого набора инвариантов, определяющих граф с точностью до изоморфизма.

3.3 Тривиальные и полные графы

Граф, состоящий из одной вершины, называется тривиальным. Граф, состоящий из простого цикла с kвершинами, обозначается С_k .