Курсовая работа: Ігри з природою

2. Існує стратегія (а) , краща ніж (а) . Це означає, що співвідношення (1.2.3.1) для стратегії (а) буде справедливе при всіх . В цьому випадку стратегію (а) потрібно виключити з розгляду на користь стратегії (а) , тобто вважати її неприпустимою. Допустимі стратегії зручно розглядати в термінах S- гри. Оскільки в S- грістратегія статистика визначається точкою S опуклої оболонки S* , а втрати при різних визначаються координатами цієї точки, то стратегія, що визначається точкою S , буде допустимою, якщо не існує іншої точки , у якої всі координати будуть менше відповідних координат точки S . Метод знаходження допустимих стратегій розберемо для випадку, коли простір станів природи складається з елементів і . На мал. 1.2.3.1 показана опукла область S* , що відповідає цьому випадку.

Розглянемо стратегію, що визначається точкою , яка розташовується всередині області S* . Ця стратегія не є допустимою, оскільки всі точки, що лежать на відрізку OS ₁ усередині S* , визначають кращі стратегії, ніж . Якнайкращою з них є стратегія S , що належить нижній лівій межі області S* . [5]

Тому всі внутрішні точки можна виключити на користь точок, що належать нижній лівій межі області S* , відзначеної на малюнку жирною лінією. Проте зсув точки уздовж цієї межі не дає яких-небудь переваг, оскільки при цьому зменшуються втрати, що відповідають одному стану природи, але збільшуються втрати, що відповідають іншому стану природи. Тому точки, що належать нижній лівій межі області S* і визначають допустимі стратегії статистика.

S

Мал . 1.2.2.1 Допусти мі стратег ії в S - грі

1.3 Принципи розв ’ язання статистичних задач

Розглянемо гру з природою: у нас (сторона А ) є т можливих стратегій ; що стосується обстановки, то про неї можна зробити п припущень: . Розглянемо їх як «стратегії природи». Наш виграш при кожній парі стратегій заданий матрицею (таблиця 1.3.1).[2, c. 196-199]

Таблиц я 1.3.1

Необхідно вибрати таку стратегію гравця А (чисту, або можливо, змішану, якщо це можливо), яка є більш вигідною в порівнянні з іншими.

Найпростіший випадок вибору розв’язку в грі з природою — це випадок коли якась із стратегій гравця А перевершує інші («домінує» над ними), як, наприклад, стратегія А₂ в таблиці 1.3.2.

Тут виграш при стратегії А₂ при будь-якому стані природи не менше ніж при інших стратегіях, а при деяких — більше; значить потрібний вибирати саме цю стратегію.

Таблиц я 1.3.2

Якщо навіть в матриці гри з природою немає однієї домінуючій над всіма іншими стратегії, все ж таки корисно подивитися, чи немає в ній дублюючих стратегій і поступливих іншим за всіх умов. Але тут є одна тонкість: так ми можна зменшити тільки число стратегій гравця А , але не гравця П. Припустимо, що «чищення» матриці проведено, і ні дублюючих, ні явно невигідних гравцю А стратегій в ній немає. Припустимо, що виграш при нашій стратегії A_i і стані природа більше, ніж при нашій стратегіїA_k і стані природи : >. Але за рахунок чого більше? За рахунок того, що вдало вибрали стратегію A_i ? Необов'язково. Можливо, просто стан природи вигідніше, ніж . Наприклад, стан природи «нормальні умови» для будь-якої операції вигідніше, ніж «повінь», «землетрус» і т.п. Бажано ввести такі показники, які не просто давали б виграш при даній стратегії в кожній ситуації, але відображали б «вдачність» або «невдачність» вибору даної стратегії в даній ситуації. З цією метою в теорії рішень вводиться поняття «ризику». Ризиком гравця А при користуванні стратегією A_i в умовах називається різниця між виграшем, який ми отримали б, якби знали умови , і виграшем, який ми отримаємо, не знаючи їх і вибираючи стратегію A_i :

Для прикладу візьмемо матрицю виграшів ()(таблиця 1.3.3) і побудуємо для неї матрицю ризиків ( ) (таблиця 1.3.4).При погляді на матрицю ризиків (таблиця 1.3.4) стають яснішими деякі риси даної «гри з природою». Так, в матриці виграшів ()(таблиця 1.3.3) в другому рядку перший і останній елементи були рівні один одному: .

Таблиц я 1.3.3

	4	8	6	9

Таблиц я 1.3.4

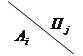Проте ці виграші зовсім не рівноцінні в значенні вдалого вибору стратегії: при стані природи могливиграти найбільше 4, і вибір стратегії А₂ майже абсолютно добрий; а ось при стані могли б, вибравши стратегіюА₁ отримати на цілі 6 одиниць більше, тобто вибір стратегії А₂ дужепоганий. Ризик — це «платня за відсутність інформації»: в таблиці 1.3.4r₂₁ = 1, r₂₄ = 6. Природно, хотілося б мінімізувати ризик, супроводжуючий вибір розв’язку.

Найпростіший випадок невизначеності — це «доброякісна або стохастична невизначеність», коли стани природи мають якісь вірогідності і цю вірогідності нам відомі. Тоді вибираємо ту стратегію, для якої середнє значення виграшу, узяте по рядку, максимально:

А середній ризик повинен бути мінімальним:

Припустимо, що вірогідність у принципі існує, але невідомі. Іноді в цьому випадку припускають всі стани природи рівноімовірними (так званий «принцип недостатньої підстави» Лапласа), але взагалі-то це робити не рекомендується. Все-таки звичайно більш менш ясно, які стани більш, а які — менш вірогідні. Для того, щоб знайти орієнтовні значення вірогідностей , можна, наприклад, скористатися методом експертних оцінок.

Візьмемо випадок «поганої невизначеності», коли вірогідність станів природи або взагалі не існують, або не піддаються оцінці навіть приблизно. Тут все залежить від точки зору на ситуацію, від позиції дослідника, від того, якими бідами загрожує невдалий вибір рішення. Опишемо декілька можливих підходів, точок зору (або, як то кажуть, декілька «критеріїв» для вибору рішення).

1. Максимінний критерій Вальда. [2, c. 196] Згідно цьому критерію гра з природою ведеться як гра з розумним, причому агресивним супротивником, що робить все для того, щоб перешкодити нам досягти успіху. Оптимальною вважається стратегія, при якій гарантується виграш у будь-якому випадку не менший, ніж «нижня ціна гри з природою»:

.