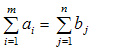Курсовая работа: Информационная система для автоматизации операций в отношениях между поставщиком и заказчиком

Рис.13 Вид таблицы

Рис.14 Таблица в режиме конструктор

Рис.15 Вид таблицы

3. Математическая модель, предмета разработки и алгоритм ее решения

Под названием транспортная задача объединяется широкий круг задач с единой математической моделью. Данные задачи относятся к задачам линейного программирования и могут быть решены известным симплексным методом. Однако, обычная транспортная задача имеет большое число переменных и решение ее симплексным методом громоздко. С другой стороны матрица системы ограничений транспортной задачи весьма своеобразна, поэтому для ее решения разработаны специальные методы. Эти методы, как и симплексный метод, позволяют найти начальное опорное решение, а затем, улучшая его, получить последовательность опорных решений, которая завершается оптимальным решением.

Однородный груз сосредоточен у m поставщиков в объемах a₁ , a₂ ,... a_m . Данный груз необходимо доставить n потребителям в объемах b_1, b₂ ... b_n . Известны C_ij , i=1,2,...m; j=1,2,...n — стоимости перевозки единиц груза от каждого i-го поставщика каждому j-му потребителю. Требуется составить такой план перевозок, при котором запасы всех поставщиков вывозятся полностью, запросы всех потребителей удовлетворяются полностью, и суммарные затраты на перевозку всех грузов являются минимальными.

Исходные данные транспортной задачи записываются в виде таблицы:

Исходные данные задачи могут быть представлены в виде:

- вектора А=(a₁ ,a₂ ,...,a_m ) запасов поставщиков

- вектора B=(b₁ ,b₂ ,...,b_n ) запросов потребителей

- матрицы стоимостей:

Переменными (неизвестными) транспортной задачи являются x_ij , i=1,2,...,m j=1,2,...,n — объемы перевозок от i-го поставщика каждому j-му потребителю. Эти переменные могут быть записаны в виде матрицы перевозок:

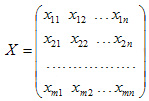
Так как произведение C_ij *X_ij определяет затраты на перевозку груза от i-го поставщика j-му потребителю, то суммарные затраты на перевозку всех грузов равны:

По условию задачи требуется обеспечить минимум суммарных затрат. Следовательно, целевая функция задачи имеет вид:

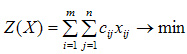
Система ограничений задачи состоит из двух групп уравнений. Первая группа из m уравнений описывает тот факт, что запасы всех m поставщиков вывозятся полностью и имеет вид:

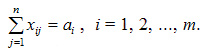
Вторая группа из n уравнений выражает требование удовлетворить запросы всех n потребителей полностью и имеет вид:

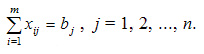
Учитывая условие неотрицательности объемов перевозок математическая модель выглядит следующим образом:

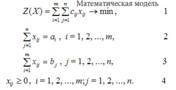
В рассмотренной модели транспортной задачи предполагается, что суммарные запасы поставщиков равны суммарынм запросам потребителей, т.е.: