Курсовая работа: Интеграционный метод Эйлера для решения линейных систем алгебраических уравнений

Матрица , при этом суть константы, вычисленные в точке линеаризации:

=

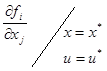
Входной сигнал при линеаризации является известной функцией времени и при фиксированном t_m на шаге h_m может считаться константой. Элементы матрицы А меняются лишь с изменением точки линеаризации.

Характеристики метода:

1. Точность. Формула x^{m +1} =x^m +h_m F(x^m ,t_m ) аппроксимирует ряд Тейлора для функции x(t_m - 1) до линейного по h члена включительно. Поэтому ε^am _i пропорциональна h_m ² . Можно сказать, что существует такое значение в интервале, при котором

ε

2. Устойчивость. Для анализа устойчивость матрицу А приводят к диагональному виду: A = PλP^-1 . Тогда система примет вид: x^’ = PλP^-1 x. Нулевое состояние равновесия системы асимптотически устойчиво при a<0, значит и метод Эйлера для этого уравнения, имеющий вид, также асимптотически устойчив. При a>0 нулевое состояние равновесия системы неустойчиво. Следовательно, система также неустойчива.

3. Шаг интегрирования. При соблюдении абсолютной или относительной устойчивости:

h<2t_min ,

В любых случаях шаг нужно корректировать по условиям точности.

эйлер линейный уравнение программа интерация

2. ОПИСАНИЕ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ

В этом разделе будут рассмотрены параметры программы и ее логическая структура.

2.1 Общие сведения

Программа написана на языке MatLAB в среде MatLAB 6.5. Для работы программы необходимо наличие операционной системы Windows 95 и выше, а также наличие среды MatLAB6.5 (на более поздних версиях среды программа не тестировалась). Программа включает в себя 4 файлов: Start.m – головной файл, необходимый для запуска программы на выполнение и построения графика функций и ошибок, Fun.m – содержит ОДУ для вычисления, FunT – функция вычисления точного решения системы, RK1.m – содержит решение системы методом Эйлера.

2.2 Функциональное назначение

Программа предназначена для решения систем линейных ОДУ методом Эйлера. Вывод решения производится по графикам. На них отображены зависимости решения от времени интегрирования.

2.3 Логическая структура

Работу программы можно представить с помощью схемы, изображенной на рис.1:

Рис. 1. Блок-схема программы

Рассмотрим каждый из этапов работы программы подробнее.

Ввод исходных данных осуществляется путем внесения изменений в текст программы.

Далее программа вызывает RK1.m, где происходит решение системы методом Эйлера, следуя алгоритму:

1. задание исходных данных, инициализация переменных

2. вычисление значений х, если выбран способ решения с переменным шагом, то происходит вычисление шага и его сравнение с максимальным, который задан изначально

3. формирование t_out, y_out, в которые заносятся соответственно время интегрирования и значения х.

Далее происходит вызов FunT, где вычисляется точное решение системы.

После чего происходит построение графиков.

2.4 Входные данные