Курсовая работа: Интеграционный метод Эйлера для решения линейных систем алгебраических уравнений
a) линейное ОДУ
b) шаг интегрирования
c) допустимая ошибка аппроксимации
d) начальные значения х
2.5 Вызов и загрузка
Вызов программы происходит через среду MatLAB. Для этого надо указать директорию доступа к файлам программы и ввести в командную строку имя головного файла – start.m. Программа занимает 1.5 Кб места жесткого диска (начальное время интегрирования). При вычислении результата и построении графиков используется незначительный объем памяти.
2.6 Выходные данные
Выходная информация представляется в графическом виде. Значения всех переменных можно просмотреть через среду MatLAB.
3. ОПИСАНИЕ ТЕСТОВЫХ ЗАДАЧ
В ходе тестирования программ, реализующих метод Эйлера для обычных и жестких линейных ОДУ, исследовалось влияние шага интегрирования на ошибку аппроксимации и число итераций. Для этого исследования вводились различные значения.
3.2 Для обычных линейных ОДУ
Программа тестировалась на системе:
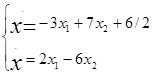
| Величина шага | Ошибка аппроксимации | число итераций |
| 0,1 | 0,0099 | 256 |
| 0,01 | 0,01 | 1932 |
| 0,001 | 0,0073 | 358 |
| 0,0001 | 0,01 | 2569 |
| 0,00001 | 0,0015 | 1 |
При решении этой же системы c переменным шагом число итераций возросло до 2530, при этом ошибка аппроксимации составила 0,0099.
3.3 Для жестких ОДУ
Программа тестировалась на системе:
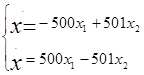
Число итераций при решении системы составило 2016, ошибка аппроксимации равна 0,01.
Величина шага | Ошибка аппроксимации | число итераций |
| 0,1 | 0,0091 | 157 |
| 0,01 | 0,01 | 1169 |
| 0,001 | 0,01 | 7129 |
| 0,0001 | 0,01 | 25258 |
| 0,00001 | 0,0012 | 1 |
В Приложении 2 содержаться графики итераций для шага 0,01 и 0,001 для обычных систем и для шага 0,01 – для жестких.
4. АНАЛИЗ РЕЗУЛЬТАТОВ. ВЫВОДЫ
Проведя анализ результатов тестирования, можно сказать, что наиболее эффективна программа при шаге интегрирования равном 0,00001, так как именно тогда ошибка аппроксимации минимальна и число итераций равно 1.
Видно, что чем меньше ошибка аппроксимации, тем меньше итераций требуется для решения.
При шаге 0,00001 на графики были в виде прямых, что можно списать на округление значений при вычислении.
Исходя из графиков, также можно сказать, что решения совпадают, однако, при заданном максимуме итерационного шага количество итераций в этом методе значительно превышает количество итераций при том же шаге в методе с постоянным шагом, практически не влияя при этом на ошибку аппроксимации.
Проанализировав результаты решения жесткой системы, можно сказать, что плохая обусловленность матрицы делает практически непоказательным графическое решение, так как по нему очень сложно судить о поведении обеих переменных, в силу того что на фоне одной из них (х2 ) не заметна другая.
То есть:
· величина шага влияет на число итераций
· точность решения зависит от величины шага