Курсовая работа: Использование корреляционных связей в комплексе с ядерно-геофизическими методами

В общем, регрессия может быть однозначно описана, если известей вид уравнения и значения коэффициентов при неизвестных. Остановимся на анализе линейной регрессии. В системе двух уравнений линейной регрессии коэффициенты а1 и а2, определяют положения начальных точек уравнений и называются коэффициентами пересечения или свободными членами уравнений [2, 34, 44, 48]. При а1 = а2, =0 уравнения исходят из начала координат.

Степень зависимости (тесноты связи) случайных величин определяется коэффициентами линейной регрессии - в1 и в2, геометрически они представляют собой тангенсы углов наклона прямых регрессии к осям абсцисс и ординат (a и b ). В общем случае прямые регрессии имеют общую точку пересечения с координатами в виде математических ожиданий величин X и У , а угол g между ними изменяется в пределах (0-90°) и характеризует также связь между величинами (чем меньше g , тем теснее связь, g =0 связь - функциональная, т.к. обе линии сливаются, в1= 1 / в2 или в1× в2=1)

Основными числовыми характеристиками двумерного распределения случайных величин являются показатели их связи: для линейной регрессии - коэффициент корреляции и корреляционный момент (ковариация); для нелинейной регрессии - корреляционное отношение [2, 44, 75].

Коэффициентом корреляции r между случайными величинами х и у называется математическое ожидание произведения их нормированных отклонений:

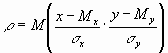
где Мх и Му – центры распределения величин х и у, и - их дисперсии. Коэффициент корреляции r может быть представлен в следующей форме:

Величина М(х-Мх)(у-Му) называется корреляционными моментом (ковариацией) – COV (x;y).

Коэффициент корреляции – величина безразмерная с пределами изменения - ± 1. При r =0 линейная связь полностью отсутствует. Знак r (+) или (-) указывает на характер связи (прямая или обратная).

Равенства | r | =1 означает наличие линейной функциональной зависимости между величинами х и у.

Несмещенными и состоятельными оценками математических ожиданий Х= Мх и У=Му служат эмпирические средние значения:

;

Несмещенными и состоятельными оценками дисперсии и служат эмпирические дисперсии:

Несмещенной и состоятельной оценкой корреляционного момента служит эмпирический корреляционный момент (ковариация)

По этим оценкам определяют эмпирический коэффициент корреляции:

который дает состоятельную, но смещенную оценку теоретического коэффициента корреляции r (смещение, при n>50 составляет менее 1%).

Значимость r проверяется путем сравнения величины |r| × с его критическими значениями Н при заданной надежности r . При |r| × > H гипотеза о корреляционной связи подтверждается с надежностью r . Доверительные оценки r сложны и разработаны для случая нормального совместного распределения вероятностей величин X и У. Для приближенных доверительных оценок истинного значения коэффициента корреляции имеются номограммы[322]. Эмпирический коэффициент r может быть оценен оперативно графическим способом [44]. Доверительные интервалы для эмпирического коэффициента корреляции r, при малом количестве наблюдений n позволяет определить следующее преобразование, предложенное Р. Фишером:

Величина Z при небольших n с хорошим приближением следует нормальному закону cо средним

и дисперсией

Это позволяет построить доверительный интервал [ Z1, Z2] для MZ по формуле:

откуда следует, что истинное значение r с той же доверительной вероятностью ( 1-a ) заключено в пределах:

th Z1 < r< th Z2

где th - гиперболический тангенс аргумента, определяемый по таблицам. Использование Z-преобразованной величины r-оказывается более предпочтительным [76]. Параметры эмпирической прямой регрессии у на х оцениваются по формулам: