Курсовая работа: Использование корреляционных связей в комплексе с ядерно-геофизическими методами
y = во× ро(х) + в1× р1(х) +…вvрv(x), где ро(х)=1, р1(х)=(х-` х),
Параметры вj не зависят от степени искомого полинома и определяются по формуле:
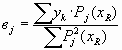(j=0,1….n)
Истинные значения параметров вj с надежностью P лежат в доверительных интервалах:
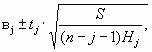где tj =t(P,R) из таблиц распределения при числе степеней свободы R=n-j-1,
есть сумма квадратов отклонений опытных точек от расчетных, 
.
Все измерения предполагаются равноточными и независимыми с нормально распределенными ошибками. При оценке геохимических систем с парагенетическими корреляционными связями применяется метод множественной линейной корреляции для трех-шести компонент, уравнение множественной регрессии которого представляет линеаризированную функцию: 
, где xi - значения i -ого признака.
Найденное уравнение наилучшим образом, в смысле метода наименьших квадратов, соответствует имеющимся эмпирическим данным. Задача сводится к вычислению коэффициентов регрессии ao,a1,…aR по совокупности N наблюдений переменных x1,x2,…xm и зависимой переменной y. При вычислениях на ЭВМ определяются следующие показатели [44]:
Вычисление сумм взаимных произведений отклонений всех переменных
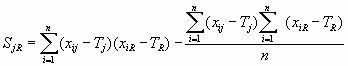
где j = 1, 2, 3,… m; 
R=1, 2, 3,… m;
2. Вычисление средних для всех переменных
3. Вычисление парных эмпирических коэффициентов корреляции
где j = 1, 2, 3,… m; R=1, 2, 3,… m;
4. Вычисление стандартных отклонений для всех переменных
5. Подбор обратной матрицы парных эмпирических корреляционных коэффициентов, которая при умножении на данную матрицу дает единичную матрицу.
R . R-1 = R-1 .R = E
6. Вычисление коэффициентов регрессии 
где Sy - стандартное отклонение зависимой переменной;
Sj - стандартное отклонение J -ой независимой переменной;
rij - парная корреляция i -ой независимой переменной с зависимой
переменной;
rij-1 - обратная корреляция независимых переменных.
7. Вычисление свободного члена 
где ` y -среднее значение зависимой переменной y;
` xj - среднее значение j -той независимой переменной.