Курсовая работа: Исследование метода продолжения решения по параметру для нелинейных САУ
j= [30*0.0001*exp (30*x) +1];
end
3. Описание тестовых задач
Исследуем влияние вектора начальных приближений на время счета, число итераций и сходимость метода.
Начальное приближение x0 =0 , заданная точность edop=0.1, dt=0.1.
График значений xна каждом шаге итерации
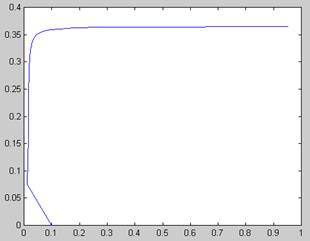
График ошибки
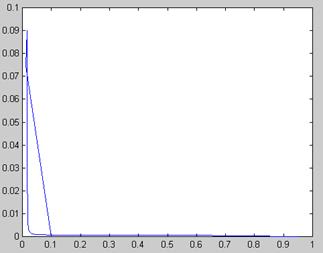
Результат выполнения программы: количество итераций=60, время счета=4с.
Начальное приближение x0 =0.3 , заданная точность edop=0.1, dt=0.1.
График значений xна каждом шаге итерации
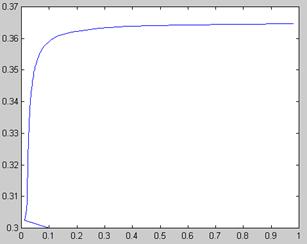
График ошибки
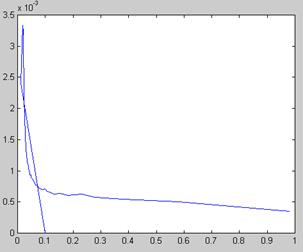
Результат выполнения программы: количество итераций=50, время счета=3,5с.
Начальное приближение x0 =0.35 , заданная точность edop=0.1, dt=0.1
нелинейный корень продолжение решение
График значений xна каждом шаге итерации
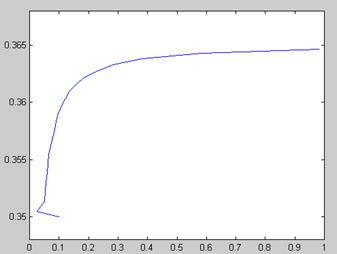
График ошибки
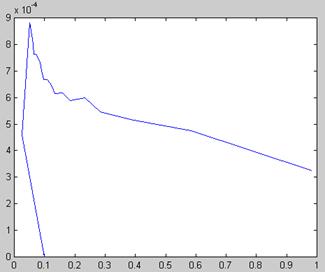
Результат выполнения программы: количество итераций=22, время счета=2с.
Исследуем влияние заданной точности решения на время счета, число итераций и сходимость метода.
Начальное приближение x0 =0, заданная точность edop=0.05 , dt=0.1.
График значений xна каждом шаге итерации
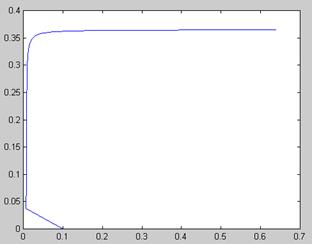
График ошибки
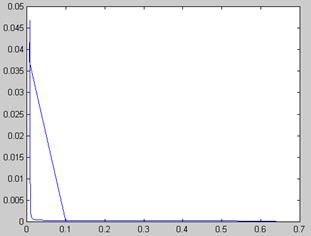
Результат выполнения программы: количество итераций=119, время счета=1,5с.