Курсовая работа: Исследование работы скважины

1. Распределение давления в водоносной и нефтеносной областях найдем из уравнений (1) и (3), подставив в них значения давления на границе раздела p из (5). В результате получим

, при ;(6)

, при . (7)

2. Скорости фильтрации жидкостей определяем

при ; (8)

при. (9)

Из формул (8) и (9) видно, что скорости фильтрации, как воды, так и нефти растут во времени (так как знаменатель в указанных формулах уменьшается во времени).

3. Дебит скважины Q найдем, умножив скорость фильтрации на площадь :

(10)

(11)

При постоянной депрессии дебит скважины увеличивается во времени, т.е. с приближением к ней контура нефтеносности. Такое самопроизвольное увеличение дебита нефти перед прорывом воды в скважину подтверждается и промысловыми наблюдениями. При формула (10) превращается в формулу Дюпюи.

4. Время прохождения частицей жидкости заданного участка от до определяем

(12)

5. Время вытеснения всей нефти водой T найдем, подставив в уравнение (12) . В результате получим (пренебрегая по сравнению с )

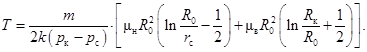(13)

6. Определяем коэффициент продуктивности по формуле

. (14)

7. Для определения линейности фильтрации определим число Рейнольдса по формуле Щелкачёва В.Н.:

, (15)

скважина фильтрация нефть плоскорадиальный

где кинематический коэффициент вязкости воды, определяемый по формуле[1]

. (16)

2. Математический расчет

2.1 Исследование фильтрации при различном положении радиуса водонефтяного контакта

Рассчитаем коэффициент фильтрации по формуле (11) взяв значения из графика на рисунке 2:

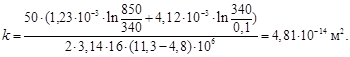
Для определения закона фильтрации определим скорость фильтрации воды у скважины по формуле(2):