Курсовая работа: Итерационный метод решения проблемы собственных значений

Данные, полученные при выполнении программы:

y = 0.1496 m = 25 L1 = -5.5251 t = 0

0.0135

0.7866

-0.5989

График значений собственного числа заданной матрицы за время итерационного процесса/

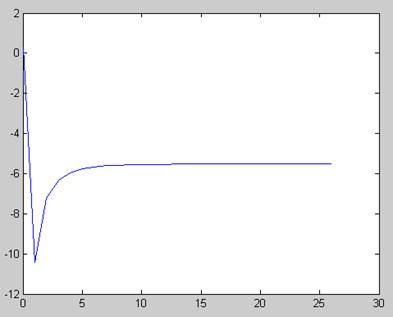
График значений собственного вектора, соответствующего собственному числу

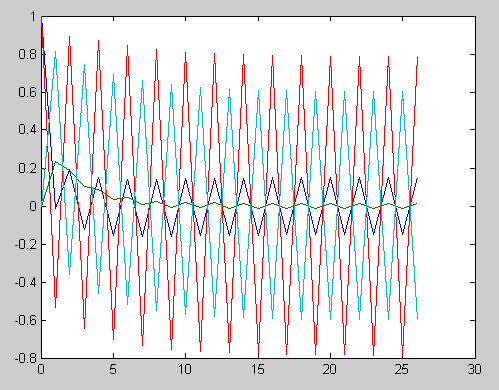
Рассмотрим другие примеры:

Исходные данные:

yn=[1,1,1];

L1= 0.01

edop=0.00001;

a=[1 1 1;

2 3 4;

0 4 0];

Найдем собственные значения исходной матрицы, используя функцию eig. Получим

L1= 6.2085

0.4794

-2.6879

Полученный результат:

y = 0.2565 m =13 L1 =6.2085 t =0

0.8125

0.5235

График значений собственного числа заданной матрицы за время итерационного процесса

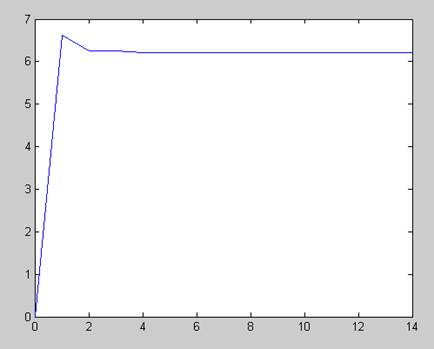
График значений собственного вектора, соответствующего собственному числу

Так при задании начального приближения, находящегося далеко от точного решения, итерационный процесс расходится. Если значение начального приближения выбрано близко к точному решению, то итерационный процесс сходится, и чем ближе вектор начального приближения к точному решению, тем за меньшее число итераций сходится итерационный процесс.