Курсовая работа: Изучение функций в курсе математики VII-VIII классов

В современном школьном курсе математики в итоге длительных методических поисков в качестве ведущего был принят генетический подход к понятию функции. Одновременно учитывается все ценное, что можно извлечь из логического подхода. Исходя из этого при формировании понятий и представлений, методов и приемов в составе функциональной линии система обучения строится так, чтобы внимание учащихся сосредоточивалось, во-первых, на выделенных и достаточно четко разграниченных представлениях, связанных с функцией, и, во-вторых, на установлении их взаимодействия при развертывании учебного материала. Иными словами, в обучении должна быть выделена система компонентов понятия функции и установлена связь между ними. В эту систему входят такие компоненты:

- представление о функциональной зависимости переменных

величин в реальных процессах и в математике;

- представление о функции как о соответствии;

- построение и использование графиков функций, исследование функций;

- вычисление значений функций, определенных различными

способами.

В процессе обучения алгебре все указанные компоненты присутствуют при любом подходе к понятию функции, но акцент может быть сделан на одном из них. Как только что мы отметили, функциональный компонент является основой введения и изучения понятия функции. На этой основе при организации работы над определением вводятся и другие компоненты, проявляющиеся в различных способах задания функциональной зависимости и ее графического представления.

Рассмотрим теперь взаимодействие компонентов на примере, относящемся к формированию прикладных умений и навыков.

Пример 1. С мороза в комнату внесли банку со льдом и стали наблюдать за изменением температуры вещества в банке: лед постепенно таял, когда он растаял весь, температура воды стала повышаться, пока не сравнялась с температурой в комнате. На рисунке изображен график зависимости температуры от времени.

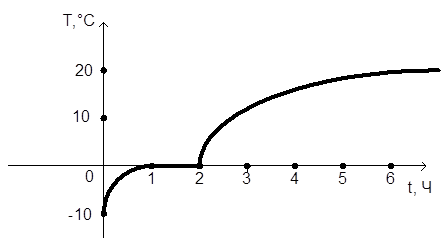
Ответьте на вопросы: а) Какова исходная температура льда? б) За какое время температура льда повысилась до 0 °С? в) Какая температура в комнате? г) Укажите область, на которой определена функция, промежутки ее возрастания, промежуток, на котором она постоянна.

В этом примере необходимо использовать все компоненты, кроме последнего, вычислительного компонента. Процесс с самого начала представлен как функциональная зависимость. В вопросах требуется уточнить характер этой зависимости (вопрос г)), выяснить соответствующие значения функции и аргумента в определенные моменты процесса (вопросы а) и в)).

Понятие функции, в системе формирования которого должны присутствовать такие задания, сразу выступает в курсе математики как определённая математическая модель, что и является мотивировкой для его углублённого изучения.

Методика введения понятий: функции, аргумента, области определения.

Не смотря на чрезвычайно большой объем, широту и сложность понятия функции, его простейший вариант дается уже в средних классах школы. Это понятие в дальнейшем играет важную роль, являясь базовым понятием в изучении алгебры и начал анализа. Начиная с 7 класса средней школы идет постепенное изучение свойств функций и функциональных зависимостей. Рассматриваются различные классы функций: начиная с простейших линейных функций и их графиков, затем следуют квадратичные функции, функции обратной пропорциональности и дробно-линейные функции. В более старших классах вводятся тригонометрические функции, и, наконец, показательные и логарифмические функции. Все эти функции рассматриваются только как функции одной переменной, причем сами переменные не выходят за рамки множества вещественных чисел.

В настоящее время, на волне педагогического поиска, стало появляться множество экспериментальных учебников для использования в школе. Наряду с добротными, толково написанными учебниками, в школы стала попадать, под предлогом апробации, масса учебников с довольно вольной трактовкой учебного материала, в том числе и глав, касающихся изучения функций. Часто нарушается логический порядок следования изучаемых разделов, допускаются ошибки при построении графиков, материал необоснованно упрощается, примитивизируется или наоборот, чрезмерно перегружается терминами и символикой.

Введение понятия функции — длительный процесс, завершающийся формированием представлений о всех компонентах этого понятия в их взаимной связи и о роли, играемой им в математике и в ее приложениях. Этот процесс ведется по трем основным направлениям:

- упорядочение имеющихся представлений о функции, развертывание системы понятий, характерных для функциональной линии (способы задания и общие свойства функций, графическое

истолкование области определения, области значений, возрастания и т. д. на основе метода координат);

- глубокое изучение отдельных функций и их классов;

- расширение области приложений алгебры за счет включения в нее идеи функции и разветвленной системы действий с функцией.

Первое из этих направлений проявляется в курсе школьной алгебры ранее остальных.

В реализации этого направления значительное место отводится усвоению важного представления, входящего в понятие функции,— однозначности соответствия аргумента и определенного по нему значения функции. Для рассмотрения этого вопроса привлекаются различные способы задания функции.

Чаще других в математике и ее приложениях применяется задание функции формулой. Все другие способы играют подчиненную роль. Именно поэтому после первого знакомства с несколькими такими способами основное внимание в обучении уделяется тем функциям и классам, которые имеют стандартную алгебраическую форму их выражения. Однако при введении понятия сопоставление разных способов задания функции выполняет важную роль. Во-первых, оно связано с практической потребностью: и таблицы, и графики, как правило, служат для удобного в определенных обстоятельствах представления функции, имеющей аналитическую форму записи. Во-вторых, оно важно для усвоения всего многообразия аспектов понятия функции. Формула выражает функцию лишь будучи включенной в соответствующую систему представлений и операций, а эта система такова, что различные компоненты понятия функции могут быть отображены наиболее естественно различными средствами.

Использование перевода задания функции из одной формы представления в другую — необходимый методический прием при введении понятия функции.

Реализация этого приема состоит в использовании системы заданий, в которых представлены все случаи такого перевода. Если ограничиться основными способами представления функции — формулой, графиком, таблицей, то получится 6 типов упражнений, при которых форма представления меняется, и 3 — при которых она остается такой же. Приведем примеры заданий первого типа — изменения формы представления:

а) Изобразить график функции у = 4х+1 на промежутке [0; 2].

б) Проверить, насколько точна таблица квадратов чисел, взяв несколько значений для аргумента и проведя расчет: x=1,35; 2,44; 9,4; 7; 6,25.

в) На рисунке изображены точки на координатной плоскости, выражающие результаты наблюдений за атмосферным давлением.