Курсовая работа: Характеристика процесса исследования
,
где Xmax – наибольшее значение признака совокупности, Xmin – наименьшее значение признака совокупности, n – количество групп в группировке.
Рассчитаем интервалы группировки:
Единицы совокупности распределяются по группам
| Значение группировочного признака | Количество единиц совокупности в группе |
| Хmin + i = X1 * (Xmin – X1 ) | |
| X1 + i = X2 * (X1 +X2 ) | |
| ………… | |
| Xn-1 + i = Xn * (Xn-1 – Xn ) | |
| Итого | N |
На основании полученных данных построим группировочную таблицу, учитывая, что округление интервала производилось в сторону увеличения, то нижняя граница последнего интервала будет больше чем наибольшее значение исходных данных:
| Численность занятых в экономике | Количество единиц в совокупности в группе |
| 53 – 1138 | 10 |
| 1138–2223 | 4 |
| 2223 – 3308 | 5 |
| 3308 – 4393 | 2 |
| 4393 – 5478 | 4 |
| 5478 – 6563 | 3 |
| Итого | 28 |
3. Расчет характеристик вариационного ряда
По полученной группировке построим вариационный ряд, рассчитаем показатели центра распределения и показатели вариации распределения. Т.к. группировка строилась по количественному признаку, то получим вариационный ряд. Он состоит из вариант (отдельные значения варьируемого признака в совокупности) и частот (количество единиц совокупности с данным значением признака).
К показателям центра распределения относятся средняя арифметическая, мода, медиана.
Средняя арифметическая рассчитывается по формуле:
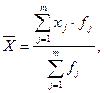
где m – количество групп; xj – варианты; fj – частоты.
В интервальных рядах вместо вариант xj используется середина интервала 
.
Найдем середину каждого из интервалов. Она находится по формуле:
,
где x верх – верхняя граница интервала; x ниж – нижняя граница интервала.
Рассчитаем середину каждого интервала:
Рассчитаем среднюю арифметическую:
Таким образом, 2572 тыс. чел. – наиболее характерное значение численности населения, занятого в экономике.
Следующим показателем центра распределения является мода. В интервальных рядах по наибольшей частоте определяется модальный интервал, а затем рассчитывается мода по формуле:
где X 0 - нижняя граница модального интервала; f Mo – частота модального интервала; f Mo-1 – частота предмодального интервала; f Mo+1 – частота послемодального интервала; i – величина модального интервала.
Модальным интервалом является первая группа в группировочной таблице. Рассчитаем моду:
Таким образом, значение 505 тыс. чел. – наиболее часто встречаемое среди занятых в экономике.
Далее находим медиану. В интервальных рядах медиана равна варианте, накопленная частота которой больше либо равна половине объема совокупности (f / Me
). Накопленная частота (f /) в каждой группе рассчитывается сложением частоты в своей группе с частотами всех предыдущих групп. Медиана находится по формуле: