Курсовая работа: Характеристика процесса исследования
где X 0 – нижняя граница медианного интервала; f Me-1 / – накопленная частота предмедианного интервала; f Me – частота медианного интервала; i – величина медианного интервала.
Половина объема совокупности равна 14 (
). Медианным интервалом является вторая группа, т. к. ее накопленная частота равна 14. Теперь рассчитаем медиану:
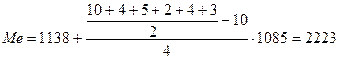
Половина из обследованных признаков меньше 2223 тыс. чел., а другая половина больше.
Теперь рассчитаем показатели центра распределения. К ним относятся: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, дисперсия, коэффициент вариации.
Размах вариации рассчитывается по формуле:
где 
– наибольшее и наименьшее значения признака в совокупности.
Рассчитаем размах вариации:
Среднее линейное отклонение рассчитывается как средняя арифметическая из модулей отклонений вариант от средней. Т.к. данные сгруппированы, то рассчитывается среднее линейное отклонение взвешенное:
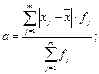
где xj – варианты;f j – частоты; 
– среднее арифметическое.
Рассчитаем среднее линейное отклонение взвешенное:
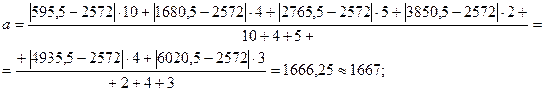
Среднее квадратическое отклонение рассчитывается как корень из средней арифметической квадратов отклонений от средней. По сгруппированным данным рассчитывается среднее квадратическое отклонение взвешенное:
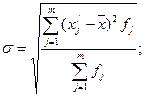
где m – количество групп; x / j – середина j -го интервала; - средняя арифметическая; f j – частота j -го интервала.
Рассчитаем седнее квадратическое отклонение взвешенное:
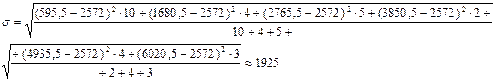
На 1667 и на 1925 тыс. чел. в среднем отличаются отдельные значения совокупности от средней численности занятых в экономике.
Взвешенная дисперсия рассчитывается по формуле:
где 
– середина интервала; – среднее арифметическое;f j – частоты.
Рассчитаем взвешенную дисперсию:
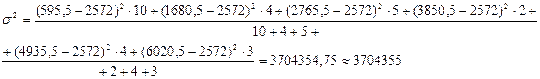
Найдем типичность средней величины через коэффициент вариации:
где - средняя арифметическая; 
- среднее квадратическое отклонение.