Курсовая работа: Кинематический и силовой анализ механизмов иглы и нитепритягивателя универсальной швейной машины

Дифференцируя это выражение по времени можно получить уравнение скорости и ускорения:

S’_в = υ_В = = ω^. r^. (sinφ + ) (7)

S’’_в =а_В = = ω^2. r^. ( scosφ + ) (8)

График перемещения точки В

График скорости точки В

График ускорения точки В

Рисунок 3

2 Определение скоростей звеньев механизмов иглы и нитепритягивателя

Если точка звена находится в движении относительно стойки и относительно подвижной точки другого типа, то определяются нормальные ускорения для обоих движений, а касатель­ные ускорения находятся графически. При этом вектор нормально­го ускорения точки при движении ее относительно стойки откла­дывается из полюса плана, а при движении относительно под­вижной точки — из конца ускорения этой точки.

При определении скоростей и ускорений задается закон движения ведущего звена. Закон движения задается частотой и направлением вращения ведущего звена. Так как ведущим звеном является кривошип 1, его частота вращения постоянна, т.е. он вращается равномерно, а, следовательно, ω_О1А = const . Направление движения ведущего звена - по часовой стрелке.

Скорости точек А (механизма иглы) и С (механизма нитепритягивателя) рассчитываются по формулам:

(9)

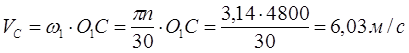(10)

Векторы скоростей и направлены пер­пендикулярно радиусам О₁ А и O₁ Cв сторону вращения этих звеньев (К_v ,м/(с^. мм) масштаб плана скоростей, который выбирается произ­вольно с учетом размеров чертежа).

(11)

(12)

План скоростей начинают строить с выбора произвольной точ­ки на чертеже, которая называется полюсом скоростей (P_V ). Скорости откладывают в соответствии с масштабом скоростей:

Скорость точки D на плане скоростей определяется путем со­вместного решения двух векторных уравнений, (она принадлежит звеньям 4 и 5) сложением векторов:

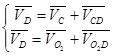(13)

При определении скорости движения точки D за полюсы вра­щения принимаются точки С и О₂ . В соответствии с правилами сло­жения векторов из конца первого вектора V_c провопят линию дейст­вия скорости . Затем из полюса P_v проводят линию дейст­вия скорости (так как первый вектор = 0). Пересечение линий действия скоростей и определяет положение точки d на плане скоростей. Далее все векторы скоростей направляют к найденной точке d и получают дли­ны векторов скоростей и в выбранном масштабе пла­на скоростей К_V .

Скорость движения точки Е, (глазка нитепритягивателя) опре­деляют по двум векторным уравнениям:

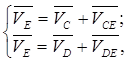(14)

где и

Соединив полюс P_V с точкой е, получают вектор скорости точ­ки Е, т.е.

V_E = V_O ^. e результате построения треугольник cde дол­жен быть подобен треугольнику CDE. Все стороны их должны быть взаимно перпендикулярны и сходственно расположены.

На основании подобия треугольников cde и CDE положение точки е на плане скоростей можно определить путем построения от линии cd треугольника cde подобного треугольнику CDE, не решая двух уравнений.

Положение точки е на плане скоростей можно найти также методом засечек.

Скорость движения точки В игловодителя определяют путем решения двух векторных уравнений:

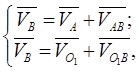(15)

В соответствии с правилами сложения векторов из конца первого вектора проводят линию действия скорости . Далее из полюса проводят линию действия скорости в направлении перемещения игловодителя (вертикально), так как первый вектор . Пересечение линий действия скоростей и определить положение точки в на плане скоростей.

3 Определение ускорений звеньев механизмов иглы и нитепритягивателя и построение плана ускорений

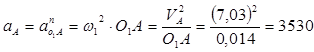(16)

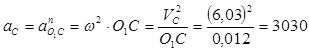(17)

При ω=const касательная составляющая ускорений = 0, = 0.

Для построения плана ускорений выбирается масштаб ускоре­ний K_a ,м/(с² *мм), который рассчитывается как:

K_a = (18)

Из произвольно выбранной точки - полюса плана ускорений откладывают (Р_а ) -откладывают вектор a_c = направленный по линии CO₁ кполюсу вращения О₁ . В результате на плане ускоренийполучают точку с, к которой направлен вектор a_o C = a_c .

Линейное ускорение точки D определяют путем решения сле­дующих векторных уравнений:

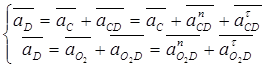, (19)

где a₀₂ = 0 (точка О₂ неподвижна).

Величины нормальных составляющих ускорений, входящих в систему уравнений (19) определяют по формулам:

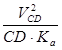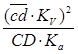= = = ; (20)

= (21)

Векторы касательных составляющих ускорений, входящих в систему уравнений (10) на плане ускорений направляют следующим образом:

В соответствии с уравнением (10) из конца вектора , т.е. точки с, на плане ускорений проводят вектор параллельно линии CD в направлении от точки D к полюсу вращения – точке С (вниз). Далее из конца вектора проводят перпендикуляр – линию действия .

Во втором векторном уравнении (10) вектор , поэтому из полюса ускорений проводят вектор параллельно линии в направлении от точки к точке (влево). Из конца этого вектора проводят перпендикуляр к нему – линию действия . Пересечение линий действий касательных ускорений определяет положение точки d на плане ускорений.

Соединив полюс плана ускорений точку с точкой d, получают вектор ускорения . При этом все ранее построенные векторы направлены к точке d.

Теорема подобия справедлива и для плана ускорений. Поэтому значительно проще найти положение точки е на плане ускорений, построив от линии cd треугольник cde, подобный треугольнику CDE на схеме механизма и сходственно с ним расположенный.