Первые два из представленных уравнений, если их рассматривать отдельно, могут показаться вполне обычными. Мы можем определить коэффициенты регрессии для каждого из этих уравнений. Но в этом случае остается открытым вопрос о равенстве спроса и предложения, т.е. может не выполняться третье равенство, в котором спрос выступает в качестве зависимой переменной. Поэтому расчет параметров отдельных уравнений в такой ситуации теряет смысл.

Экономическая модель как система одновременных уравнений может быть представлена в структурной или в приведенной форме. В структурной форме ее уравнения имеют исходный вид, отражая непосредственные связи между переменными. Приведенная форма получается после решения модели относительно эндогенных (внутренних) переменных, то есть выражения этих переменных только через экзогенные (задаваемые извне) переменные и параметры модели. Например, в модели спроса и предложения эндогенными являются переменные pl, Sl, Dl, ее параметры – a1, a2, b1, b2, а экзогенных переменных в ней нет. Таким образом, в приведенной форме переменные pl, Sl, Dl, должны выражаться только через параметры модели. Подставив Sl и Dl из (1) и (2) в (3), получаем

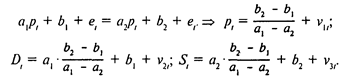
Здесь v1l, v2l, v3l - преобразованные отклонения. Мы можем оценить как среднее значение pl(т.е. ), а также , ,но из этих трех соотношений невозможно рассчитать параметры первоначальной модели a1, a2, b1 и b2(поскольку их четыре). Тем самым мы подошли к проблеме идентификации - оценке параметров структурной формы модели (в чем, собственно, и состоит наша задача) по параметрам приведенной формы. Параметры приведенной формы могут быть оценены обычным МНК, но по ним далеко не всегда может быть идентифицирована исходная модель (как, например, в описанном случае модели спроса и предложения). Для того чтобы структурная форма модели могла быть идентифицирована, вводят дополнительные предпосылки (например, о равенстве некоторых коэффициентов нулю или об их взаимосвязи между собой). Часто уже на этапе построения модели стараются выбрать такую ее форму, которая была бы идентифицируема. Такой, например, является треугольная форма модели:

(3.4)

где х - вектор объясняющих переменных, yi - i-я зависимая переменная. Нежелательна и сверхидентифицируемость модели, когда для параметров структурной формы получается слишком много со отношений из приведенной формы модели. В этом случае модель также нуждается в уточнении.

Для оценивания систем одновременных уравнений имеется ряд методов. В целом их можно разбить на две группы. К первой группе относятся методы, применяемые к каждому уравнению в отдельности. Вторая группа содержит методы, предназначенные для оценивания всей системы в целом. В пакете TSP, в частности, представлено по одному методу из каждой группы. Для оценивания отдельных уравнений можно применять двухшаговый метод наименьших квадратов (Two-Stage Least Squares). Из второй группы методов в этом пакете реализован трехшаговый метод наименьших квадратов (Three-Stage Least Squares),

Остановимся вначале на двухшаговом методе. Он применяется при наличии в оцениваемой модели лаговых переменных. Содержательный смысл двухшагового метода состоит в следующем. Как известно, МНК-оценки параметров уравнения равны b=(Х'Х)-1 X'Y, но лаговые значения у, используемые как объясняющие переменные (в этой формуле они являются частью матрицы X), заранее неизвестны. Поэтому для того, чтобы воспользоваться этой формулой, сначала, на первом шаге, определяются недостающие значения объясняемых переменных. Это в данном случае делается путем расчета МНК-оценок, т.е. строится регрессия, в которой в роли объясняемых переменных выступают только имеющиеся в исходной информации. После этого, когда исходные эмпирические данные дополнены рассчитанными значениями и сформирован полный набор данных, можно приступать к оценке искомых параметров.

Двухшаговый МНК применяется и при сверхидентифицируемости модели. В этом случае на первом шаге оцениваются параметры приведенной формы модели. С помощью уравнений приведенной формы, при заданных значениях объясняющих переменных, рассчитываются оценки зависимых переменных. Далее эти оценки подставляются в правые части уравнений модели в структурной форме, и вновь используется обычный МНК для оценки ее параметров.

Для оценки параметров всей системы уравнений в целом используется трехшаговый МНК. К его применению прибегают в тех случаях, когда переменные, объясняемые водном уравнении, в другом выступают в роли объясняющих. Так было в нашем примере с моделью спроса и предложения, где спрос и предложение, с одной стороны, определяются рыночной ценой, а с другой стороны, предложение должно быть равно спросу. При расчете параметров таких моделей необходимо учитывать всю систему соотношений. В трехшаговом методе это реализуется в три этапа. Первые два из них похожи на двухшаговый метод, т.е. производится оценка параметров в уравнениях с лаговыми переменными. В нашем примере лаговые переменные в уравнения не включены, и на этом этапе будут рассчитываться обычные коэффициенты регрессии. После этого нам нужно увязать все уравнения системы между собой. В качестве меры связи здесь выступает матрица ковариаций ошибок моделей, т.е. чтобы оценить, насколько несвязанными получатся уравнения спроса и предложения при расчете их отдельно, нужно рассчитать ковариацию ошибок е и е'. Для увеличения этой связи на следующем этапе, при очередном расчете коэффициентов регрессии учитывается матрица ковариаций ошибок. Таким приемом достигается взаимосязанность всей системы уравнений.[1]

Нелинейная регрессия

На практике часто встречается ситуация, когда априорно известен нелинейный характер зависимости между объясняемыми и объясняющими переменными. В этом случае функция f в уравнении у=(а,х) нелинейна (а - вектор параметров функции, которые нам нужно оценить). Например, вид зависимости между ценой и количеством товара в той же модели спроса и предложения: она не всегда предполагается линейной, как в нашем примере. Нелинейную функцию можно преобразовать в линейную, как это было сделано, например, логарифмированием с функцией Кобба-Дугласа. Однако не все функции поддаются такой непосредственной линеаризации. Любую дифференцируемую нужное число раз функцию можно разложить в функциональный ряд и затем оценить регрессию объясняемой переменной с членами этого ряда. Тем не менее такое разложение всегда осуществляется в окрестности определенной точки, и лишь в этой окрестности достаточно точно аппроксимирует оцениваемую функцию. В то же время оценить зависимость требуется обычно на более или менее значительном интервале, а не только в окрестности некоторой точки. При линеаризации функции или разложении её в ряд с целью оценки регрессии возникают и другие проблемы: искажение отклонений ей нарушение их первоначальных свойств, статистическая зависимость членов ряда между собой. Например, если оценивается формула

полученная путем линеаризации или разложения в ряд, то независимые переменные х и х2 связаны между собой даже не статистически, но функционально. Если исходная ошибка е здесь связана с переменной х, то добавление х2 приводит к появлению (с соответствующими коэффициентами) квадрата этой переменной и её удвоенного произведения с х, что искажает исходные предпосылки модели. Поэтому во многих случаях актуальна непосредственная оценка нелинейной формулы регрессии. Для этого можно воспользоваться нелинейным МНК. Идея МНК основана на том, чтобы минимизировать сумму квадратов отклонений расчетных значений от эмпирических, т.е. нужно оценить параметры о функции f(a,x) таким образом, чтобы ошибки еi= уi-f(а,х), точнее - их квадраты, по совокупности были минимальными. Для этого нужно решить задачу минимизации

(4.1)

Для решения этой задачи существует два пути. Во-первых, может быть осуществлена непосредственная минимизация функции F с помощью методов нелинейной оптимизации, позволяющих находить экстремумы выпуклых линий. Это, например, метод наискорейшего спуска, при использовании которого в некоторой исходной точке определяется антиградиент (направление наиболее быстрого убывания) функции F. Далее находится минимум F при движении в данном направлении, и в точке этого минимума снова определяется градиент. Процедура повторяется до тех пор, пока разница значений f на двух последовательных шагах не окажется меньше заданной малой величины. Другой путь состоит в решении системы нелинейных уравнений, которая получается из необходимых условий экстремума функции F. Эти условия - равенство нулю частных производных функции F по каждому из параметров аj., т.е.

Faj = 0,

j =1,..,m. Получается система уравнений

-2S(yi-f(a,xi))*fai'(a,xi) = 0, j = 1,..,m(4.2)

нелинейность которой обусловлена нелинейностью функции f относительно параметров аj. Эта система уравнений может быть решена итерационными методами (когда последовательно находятся векторы параметров, все в меньшей степени нарушающие уравнения системы). Однако в общем случае решение такой системы не является более простым способом нахождения вектора а, чем непосредственная оптимизация методом наискорейшего спуска.

Существуют методы оценивания нелинейной регрессии, сочетающие непосредственную оптимизацию, использующую нахождение градиента, с разложением в функциональный ряд (ряд Тейлора) для последующей оценки линейной регрессии. Наиболее известен из них метод Марквардта, сочетающий в себе достоинства каждого из двух используемых методов.

При построении нелинейных уравнений более остро, чем в линейном случае, стоит проблема правильной оценки формы зависимости между переменными. Неточности при выборе формы оцениваемой функции существенно сказываются на качестве отдельных параметров уравнений регрессии и, соответственно, на адекватности всей модели в целом.[1]

Авторегрессионное преобразование

Важной проблемой при оценивании регрессии является автокорреляция остатков е, которая говорит об отсутствии первоначально предполагавшейся их взаимной независимости. Автокорреляция остатков первого порядка, выявляемая с помощью статистики Дарбина-Уотсона, говорит о неверной спецификации уравнения либо о наличии неучтенных факторов. Естественно, для её устранения нужно попытаться выбрать более адекватную формулу зависимости, отыскать и включить важные неучтенные факторы или уточнить период оценивания регрессии. В некоторых случаях, однако, это не даст результата, а отклонения еi просто связаны авторегрессионной зависимостью. Если это авторегрессия первого порядка, то её формула имеет вид еi=rei-1 + ui(r - коэффициент авторегрессии, |r|<1), и мы предполагаем, что остатки ui в этой формуле обладают нужными свойствами, в частности - взаимно независимы. Оценив r, введем новые переменные у'i=уi -ryi-1; x'i=xi -rxi-1;^,.(это преобразование называется авторегрессионным (AR), или преобразованием Бокса-Дженкинса). Пусть мы оцениваем первоначально формулу линейной регрессии уi= а + bxi + еi. Тогда

Если величины ui.действительно обладают нужными свойствами, то в линейной регрессионной зависимости у'i= а1 + bx'i + ui автокорреляции остатков ui уже не будет, и статистика DW окажется близкой к двум. Коэффициент b этой формулы принимается для исходной формулы у = а+bх+е непосредственно, а коэффициент а, рассчитывается по формуле .

Оценки коэффициентов а и b нужно сравнить с первоначальными оценками, полученными для расчета отклонений еi Если эти оценки совпадают, то процесс заканчивается; если нет - то при новых значениях а и b вновь рассчитываются отклонения е до тех пор, пока оценки а и b на двух соседних итерациях не совпадут с требуемой точностью.

В случае, когда остатки «также автокоррелированы, авторегрессионное преобразование может быть применено ещё раз. Это означает использование авторегрессионного преобразования более высокого порядка, которое заключается в оценке коэффициентов авторегрессии соответствующего порядка для отклонений е. и использовании их для построения новых переменных. Такое преобразование вместо AR(1) называется AR(s) - если используется авторегрессия порядка s.

О целесообразности применения авторегрессионного преобразования говорит некоррелированность полученных отклонений ui,. Однако даже в этом случае истинной причиной первоначальной автокорреляции остатков может быть нелинейность формулы или неучтенный фактор. Мы же, вместо поиска этой причины, ликвидируем её бросающееся в глаза следствие. В этом - основной недостаток метода AR и содержательное ограничение для его применения.

Кроме авторегрессионного преобразования, для устранения автокорреляции остатков и уточнения формулы регрессионной зависимости может использоваться метод скользящих средних (MovingAve-rages, или МА). В этом случае считается, что отклонения от линии регрессии еi описываются как скользящие средние случайных нормально распределенных ошибок еi предполагается, что

(5.1)