Курсовая работа: Кольцевой индукционный датчик угла

Из этих уравнений следует, что при соблюдении условия первичного симметрирования выходные обмотки ВТ можно рассматривать как две независимые обмотки с выходным сопротивлением

(3.15)

и э.д.с. (рисунок 3.5):

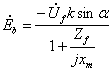; (3.16)

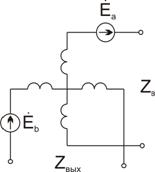
Рисунок 3.5 Схема КИДУ с исключенными обмотками возбуждения и квадратурной обмоткой

3.2 Параметры КИДУ

КИДУ характеризуется рядом величин, определяющих возможность его применения в той или иной схеме и точность работы. К величинам первой группы относятся: – номинальное напряжение возбуждения; f – частота сети; k – коэффициент трансформации или коэффициент передачи по напряжению ; – входное и выходное сопротивления; – угол сдвига фазы между вторичной э. д. с. и приложенным напряжением.

Их схемы замещения, приведенной на рисунке 3.3, получаем:

– сопротивление холостого хода;

– сопротивление короткого замыкания;

– входное сопротивление при некотором сопротивлении нагрузки;

– угол сдвига фазы между вторичной э.д.с. и приложенным напряжением, где Z_н – сопротивление источника.

Имея эти параметры, нетрудно определить любые электромагнитные величины, характеризующие работу КИДУ в схеме: потребляемые ток и мощность, выходное напряжение, оптимальную нагрузку и т.п.

Наиболее важными являются величины второй группы, характеризующие точность; они определяют, насколько реальная машина отличается от идеализированной. К этим величинам относятся:

1. Относительная амплитудная ошибка в синусоидальной зависимости вторичной э.д.с. от угла поворота ротора; она выражается в процентах или угловых минутах:

, (3.17)

где максимальная угловая ошибка в минутах

По амплитудной относительной ошибке, выраженной в %, определяются классы точности: 0,01; 0,02; 0,05; 0,1; 0,2;0,3.

2. Асимметрия нулевых точек, характеризующая неперпендикулярность обмоток статора и ротора КИДУ. Для ее определения КИДУ поочередно возбуждается со стороны первичных обмоток, и затем определяются угловые положения ротора, при которых э.д.с. вторичных обмоток равна нулю. Отклонение этих угловых положений от углов, кратных 90^о , представляет собой асимметрию нулевых точек КИДУ.

Из () следует, что для данного класса точности максимальное значение асимметрии в угловых минутах не должно превосходить

, (3.18)

где e — относительная амплитудная ошибка в процентах.

3. Остаточная э.д.с в нулевых точках (е_ос , %). Вследствие электрической и магнитной асимметрии магнитопровода от различных'технологических причин при однофазном питании КИДУ образуется эллиптическое вращающееся магнитное поле, которое индуктирует во вторичных обмотках э.д.с, сдвинутую по фазе на некоторый угол по отношению к э.д.с. от основного магнитного потока. Эта добавочная э.д.с. Может быть разложена на две составляющие (рисунок 3.6): совпадающую по фазе с основной э.д.с. и квадратурную э.д.с. Совпадающая по фазе э.д.с. компенсируется поворотом ротора, что обусловливает асимметрию нулевых точек. Квадратурная э.д.с. не может быть скомпенсирована, она представляет собой остаточную э.д.с, которая состоит из э.д.с. основной частоты и э.д.с. высших гармоник, появляющихся от нелинейности кривой намагничивания магнитопровода.

На работу КИДУ в компенсационных схемах главное влияние оказывает остаточная э.д.с. основной частоты. Ее величина не должна превосходить половины полезного сигнала, соответствующего максимальной угловой ошибке.

4. Э.д.с. квадратурной обмотки (e_k , %). В идеальном КИДУ взаимоиндукция между перпендикулярными обмотками статора (ротора) должна отсутствовать. В действительности, вследствие различного рода технологических погрешностей коэффициент взаимоиндукции между обмотками не равен нулю, что приводит к появлению э.д.с. на одной обмотке при включении в сеть другой. Эту э.д.с. называют э.д.с. квадратурной обмотки. Она состоит из основной гармоники, имеющей частоту сети, и высших временных гармоник. Э.д.с. квадратурной обмотки зависит от углового положения ротора и содержит постоянную составляющую, не зависящую от углового положения ротора, переменную составляющую, изменяющуюся с двойной периодичностью от угла поворота ротора, и зубцовые гармоники (рисунок 3.7).

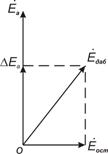
Рисунок 3.6 Векторная диаграмма остаточной э. д. с.

Рисунок 3.7 Зависимость э. д. с. квадратурной обмотки от угла по ворота ротора