Курсовая работа: Компьютерное моделирование вычислительных задач в различных средах программного обеспечения

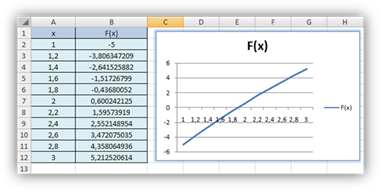
Реализация графического метода в пакете Excel.

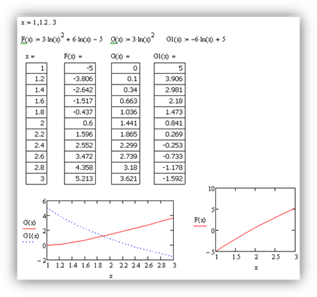?????????? ???????????? ?????? ? ?????? MathCAD.

Таким образом, искомый корень уравнения находится на отрезке [1,8;2]

2.2 Аналитический метод

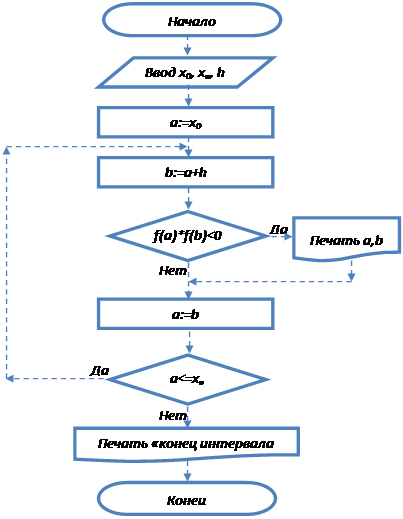Блок-схема

- Pascal.

3. Метод уточнения корней

Методы отделения корней весьма удобны и просты. Однако они дают ответ только на вопрос локализации корня и позволяют найти приближённое значение. Если же требуется найти более точное значение корня, то используют различные методы уточнении.

3.1 Метод половинного деления

Для данного метода нужен отрезок [a;b] с корнем непрерывной функции f(x) внутри и точность определения корня, которая задаётся “e”

Реализация метода в пакете Excel.

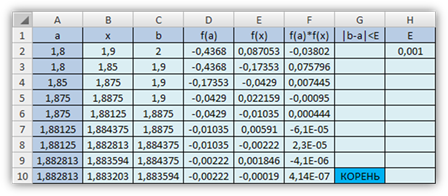
Реализация метода в пакете MathCad.

Реализация метода половинного деления в Pascal

Блок-схема

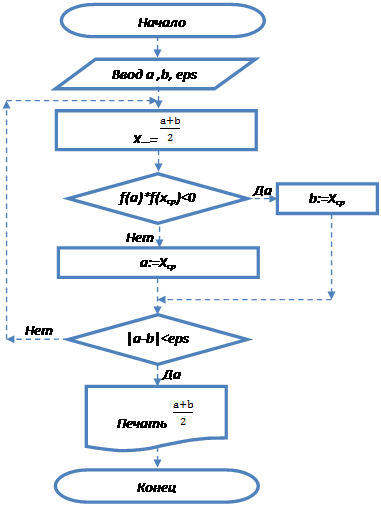
3.2 Метод последовательных приближений

Наше уравнение преобразуем к виду x=. Если на рассматриваемом интервале изоляции корня [1,8;2] ||<1 ,то расчётная формула примет такой вид : , и при этом итерационный процесс приближения к корню будет сходящимся. В нашем случае выбор расчётной формулы исходного выражения очень затруднителен, поэтому воспользуемся следующим приёмом. Введём в рассмотрение произвольный параметр л>0. Тогда функция можно представить как .

Затем просто варьируем параметр л, добиваемся условия сходимости: ||<1 на интервале изоляции корня [1,8 ; 2]. . Для выполнения сходимости на интервале изоляции корня [1,8; 2]. Производная исходного уравнения равна:.

Для этого примера запишем следующее:

.

Расчётная формула метода итерации примет вид:

Реализация метода в Pascal.