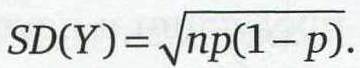Курсовая работа: Контрольные карты Шухарта контроль по доле дефектных изделий распределение параметра дискр

Дискретные величины — результаты под­счета чего-либо, например числа дефектов какого-либо изделия или числа бракованных изделий в проверенной партии. Поскольку эти величины пред­ставляют собой число появлений некоего признака (атрибута) изделий, они иногда называются атрибутами.

Существуют два коренных отличия атрибутов от факторов. Во-первых, в отличие от факторов атрибуты обладают естественной неустранимой дис­кретностью. Во-вторых, любой подсчет должен предусматривать выбор «об­ласти определения» или «множества возможных значений».

Строго говоря, непрерывные величины (факторы) тоже имеют некоторую дискретность, но ее всегда можно уменьшить, используя меньшие единицы измерения. Для счетных данных, основанных на появлении отдельных со­бытий или признаков (атрибутов), это невозможно. Атрибуты — это всегда натуральные числа. Дискретность им внутренне присуща и поэтому неустра­нима. Дискретность атрибутов обязательно надо учитывать при построении контрольных карт.

Область определения представляет собой основу для интерпретации ре­зультатов счета. Для сравнения двух дискретных величин надо, чтобы они имели совпадающие области определения. Если же их области определения не совпадают, пусть даже незначительно, то сравниваемые величины надо превратить в относительные показатели (дроби), и лишь тогда их можно осмысленно сравнивать. Такое преобразование дискретных данных в доли достигается делением результатов подсчета на их область определения.

Операции с дискретными данными предполагают ответ на два вопроса. Сильно ли мешает их неустранимая дискретность построению контрольных карт? Равны ли области определения? Когда число событий мало, дискрет­ность служит препятствием и нужны специальные методы построения кон­трольных карт. Если области определения не совпадают (хотя бы приблизи­тельно), результаты подсчета нельзя сравнивать (пока они не обращены в доли).

2.1. Простой подход к дискретным величинам

При работе с дискретными величинами каждый образец описывается одним числом. Поскольку каждый результат подсчета — это индивидуальное зна­чение, Х mR -карту можно использовать для отражения самих значений или доли этих значений. Каждое значение или доля рассматривается как наблю­дение, и скользящий размах используется для измерения вариации от одно­го значения к другому. При переходе к дискретным величинам нет проблем, если их дискретность мала относительно области определения. Иными сло­вами, когда среднее число событий (в выборке или за период времени) ве­лико, различия между факторами и атрибутами не так важны, как в случае, если это значение мало.

Насколько большим должно быть среднее число событий? Достаточ­но большим, чтобы предотвратить влияние дискретности на контрольные пределы карты или вид хода процесса. Па­губное влияние дискретности на контрольную карту начинается тогда, когда стандартное отклонение процесса становится меньше единицы измерения. Во многих случаях стандартное отклонение примерно пропорционально квадратному корню из среднего дискретного значения. В то же время наи­меньшая единица «измерения» дискретных величин всегда целое число. Объединяя эти факты, мы можем заключить, что ХmR-карту для дискретных данных можно построить во всех случаях, когда среднее значение подсчета больше единицы. Если же оно больше двух, то влияние дискретности на контрольные пределы будет ничтожным.

Эта нижняя граница (от одного до двух подсчетов на выборку) гораздо ниже обычно применяемого ограничения. Причина, по которой столь низкое ограничение приемлемо для контрольной карты, заключается в ее специфи­ке: контрольная карта призвана скорее обозначить границы гистограммы, чем описать ее форму. Дискретность атрибутов ощутимо не влияет на кон­трольные пределы (на уровне Зσ), если среднее дискретное значение не очень мало.

Это означает, что большинство атрибутов можно успешно описывать обычными ХmR-картами. Применение специальных контрольных карт может потребоваться только в том случае, если среднее дискретное значение будет очень мало.

Таким образом, можно использовать некоторые свойства дискретных данных для вычисления более узких кон­трольных пределов.

Пример №1. (см. приложение)

2.2. Карты для биномиальных величин

Любая дискретная величина должна иметь область определения. Именно она и определяет ключевое различие между двумя главными типами дискретных величин.

Рассмотрим выборку, состоящую из п элементов, отобранных в случайные моменты времени из потока продукции в некоторой точке производствен­ного процесса. Если каждое из отобранных изделий считается либо годным, либо негодным, то число негодных будет искомой дискретной величиной. Обозначим это число символом Y. Очевидно, что его область определения задается числом отобранных изделий. Оно не может быть меньше 0 и боль­ше n, следовательно, интервал [0; n] полностью определяет набор всех воз­можных значений величины Y.

Последовательность таких выборок даст ряд результатов наблюдений:

^{Y 1 , Y 2 , Y 3 , Y 4 , Y 5 ,……}

При определенных условиях для характеристики поведения этого ряда Y1,Y2,Y3,Y4,Y5,…можно использовать модель биномиальных вероятностей.

Биномиальное условие 1: область определения дискретной величины Y должна состоять из п различных значений.

Биномиальное условие 2: каждое из этих значений можно классифициро­вать как либо обладающее, либо не обладающее неким атрибутом. Обыч­но таким атрибутом служит несоответствие допускам.

Биномиальное условие 3: пусть р есть вероятность того, что объект обла­дает атрибутом. Значение р должно быть постоянным для всех п объектов любой выборки. Хотя карта проверяет, изменяется ли р от выборки к вы­борке, р должно быть постоянным внутри каждой выборки.

Биномиальное условие 4: вероятность того, что некий объект обладает атри­бутом, не зависит от того, обладал ли им предыдущий объект. (Негодные объекты обычно не образуют кластеры и независимы друг от друга.)

Когда дискретная величина удовлетворяет этим четырем условиям, для расчета контрольных пределов последовательности Y1,Y2,Y3,Y4,Y5,…можно использовать модель биномиальных вероятностей. Следовательно, мы можем использовать в наших вычислениях известное соотношение между средним и стандартным отклонением биномиального распределения. При этом не надо строить карту размахов.

Буква п здесь обозначает область опре­деления биномиальных величин, а не объем подгруппы (число значений, используемых для вычисления среднего). Биномиальная величина Y — это индивидуальное значение, единственное для каждой «подгруппы».

Рассмотрим последовательность наблюдаемых значений Y1,Y2,Y3,Y4,Y5,…

удовлетворяющую четырем условиям. Эти значения могут рассматриваться в качестве элементов биномиального распределения с параметрами n и р. Среднее для этого распределения равно

Y=np

а стандартное отклонение