Курсовая работа: Контрольные карты Шухарта контроль по доле дефектных изделий распределение параметра дискр

Выше приведены четыре условия, при которых для описания данных можно применить биномиальное распределение. Некоторые типы дискретных дан­ных и некоторые данные, выраженные в процентах, этим условиям не удо­влетворяют, и, следовательно, их нельзя анализировать при помощи р-карт и nр-карт.

Заметим, что проценты, подсчитанные на базе непрерывных величин, а не дискретных, нельзя исследовать при помощи р-карт. Разумеется, про­центы вполне могут описывать доли, однако области определения перестают быть дискретными. Поэтому наносить данные этого типа на р-карты не име­ет смысла. Для их анализа больше подойдут карта индивидуальных значений и скользящих размахов или карта средних значений и размахов.

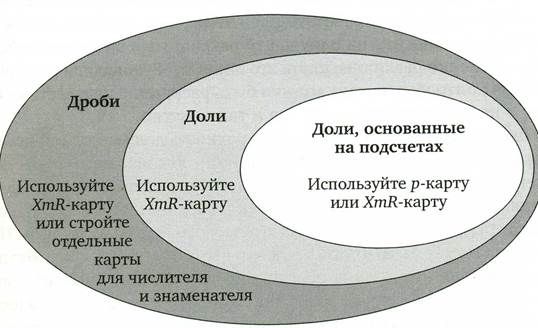
РИС . 7. Количественные характеристики, обычно выражаемые в процентах

Точно так же дроби, которые не являются долями, не годятся для р-карт. Все доли — дроби, но не все дроби — доли. Дробь можно считать долей тог­да, когда знаменатель будет описывать область определения для значений числителя.

Многие дроби, используемые в промышленности,—это не доли. Например, отношение числа переделанных изделий к общему числу произведенных в этот день изделий. Это отношение может быть для чего-то полезно, но это не доля, объем произведенной сегодня продукции не влияет на сегодняшние переделки. Единственный способ построения карт для таких данных — использование методов, разработанных для факторов. Более того, для таких данных возника­ют необычные карты. Описанная выше контрольная карта для дроби выска­кивала из статистически управляемого состояния и вверх, и вниз за два по­следовательных дня. Причиной этого скачка стала авария, из-за которой всепереключились с производства на переделку. Таким образом, в первый из этих двух дней знаменатель был очень маленьким, и дробь стала очень большой. На следующий день, когда с переделкой было покончено, числитель стал очень маленьким, и это повлияло на значение дроби. В общем, всегда лучше на­носить на карту индивидуальные значения, а не дроби, как в этом примере.

Другая ситуация, которая не удовлетворяет условиям применимости мо­дели биномиальнных вероятностей, возникает в тех случаях, когда доля негодной продукции непостоянна. В частности, и р-карты, и nр-карты под­разумевают систему, имеющую стабильную долю негодной продукции, если процесс статистически управляем. Из этого предположения следует, что вы­борки, имеющие заведомо различные значения р, не стоит смешивать на одной карте. Примерами могут служить выборки, представляющие разные станки, разные линии или смены, о которых заранее известно, что они име­ют разные доли негодной продукции. В таких случаях надо для каждой груп­пы выборок вести отдельные карты. В то же время, если предполагается, что различные станки должны работать идентично, точки, относящиеся к этим станкам, можно наносить на одну карту различными символами. Если эти станки существенно различны, карта это покажет. Руководящим принципом организации контрольных карт должно быть раскрытие неизвестных сторон процесса, а не демонстрация того, что и так понятно.

Еще один случай, при котором неоднородность доли негодной продукции от выборки к выборке не будет постоянной, встречается, когда область определения становится чрезмерно большой. Когда п выражается тысячами, то практически невозможно получить как р-карты, так и nр-карты, которые показывали бы разумную степень статистической управляемости. Причин этого явления может быть много, но почти все они связаны с корректностью постановки задачи: что именно подсчитывается? Если некий контролер про­веряет всю продукцию подряд, то может возникнуть проблема усталости: то, что кажется негодным в 9 утра, к концу рабочего дня может показаться вполне приемлемым. Итак, даже если поток выходящей с конвейера продукции имеет постоянную долю негодных изделий, контрольная карта этого постоян­ства может и не заметить. Если работает много контролеров, то возникает проблема вариации «от контролера к контролеру» в дополнение к проблеме усталости. Эта проблема делает весьма сомнительным использование р-карт для 100% данных. Большие области определения создают узкие пределы, что приведет к ложным сигналам тревоги и побуждает людей к поиску особых причин в процессе, тогда как истинная проблема заключается в контроле и подсчете или же в предположении о модели биномиальных вероятностей. Для данных такого вида гораздо лучше обычная ХmR-карта.

Пример №4 (см. приложение).

Наконец, в ситуациях, когда негодные изделия появляются группами, использовать карты для дискретных величин не следует. В этом случае не удовлетворяется условие 4 и, следовательно, нельзя применять биноми­альную и пуассоновскую вероятностные модели. Когда негодная продукция образует кластеры, можно использовать 100%-ный контроль для отбраков­ки и нанести данные на карту хода процесса. Но будет неверным нанести на эту карту контрольные пределы, используя биноминальную или пуас­соновскую модель. Когда присутствует группировка данных и 100%-ный контроль, карты для дис­кретных величин почти наверняка укажут на статистическую неуправляе­мость, безотносительно к тому, насколько хорош или плох исследуемый процесс на самом деле.

2.5. Карты для данных, основанных на распределении Пуассона.

Для биномиальных величин каждое изделие может быть годным или негод­ным. Такое разделение становится проблемой, если объекты очень сложны или непрерывны. Рассмотрим автомобиль. Его довольно трудно однозначно назвать годным или негодным. При имеющейся его сложности любой авто­мобиль был бы несоответствующим. В таком случае возникает вопрос: «Сколько дефектов в принципе может быть?» Следующий пример — рулон ткани. Один-единственный дефект в большинстве случаев не сделает этот рулон непригодным для использования. Однако чрезмерное число дефек­тов — достаточная причина для признания этого рулона некачественным.

В подобных случаях можно сосчитать сами дефекты. Результаты таких подсчетов будут иметь свои области определения, но их природа будет со­вершенно иной, чем в случае с биномиальной моделью. Для примеров выше, области определения — это, соответственно, весь авто­мобиль или весь рулон ткани. Хотя область определения в каждом из этих случаев состоит из одной явно определенной сущности (автомобиль или рулон), подсчитываемая величина (число дефектов) не ограничивается ну­лем и единицей. Такая дискретная величина может принимать огромные значения, а область определения изменилась от «числа отдельных объектов» до «ограниченной области пространства, времени или изделия».

Другой способ различать биномиальные и пуассоновские величины мож­но сформулировать при помощи следующего принципа. Для биномиальных величин можно сосчитать либо число годных, либо число негодных изделий. Для пуассоновских величин можно сосчитать только число дефектов, но ни в коем случае не «число недефектов».

Вот предварительные условия применения пуассоновского распределения:

Пуассоновское условие 1. Подсчет описывает число событий.

Пуассоновское условие 2. Эти дискретные события встречаются в хорошо

определенной конечной области пространства, времени или изделия.

Пуассоновское условие 3. Эти события случаются независимо друг от друга

и их вероятности прямо пропорциональны раз­мерам областей определения. (Это означает, что вероятность события не зависит от того, какую часть пространства, или времени, или продукта вы выбрали как область определения — вероят­ность события однородна в каждой выборке.)

Первые два условия легко проверить для каждого конкретного случая, однако их выполнения недостаточно для суждения об использовании модели Пуассона. Именно третье условие существенно для использования распреде­ления Пуассона.

Стандартное отклонение величины, распределенной по закону Пуассона, равно квадратному корню из ее среднего значения. Это свойство позволит нам обойтись без карты размахов и определить контрольные пределы лишь по одной статистике положения — среднему.

Еще раз напомним, что для сравнения отдельных результатов подсчетов они все должны иметь одну и ту же область определения. Если это требо­вание выполнено, мы можем выразить среднее число обнаруженных де­фектов так:

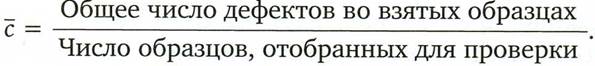
Вот формулы для вычисления контрольных пределов с-карты:

верхний контрольный предел: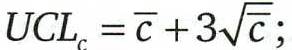

центральная линия: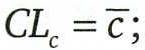

нижний контрольный предел:

Когда распределение Пуассона характеризует последовательность под­счетов, эти пределы определяют их естественную вариацию. Удовлетвори­тельные результаты можно получить, только если все три условия распреде­ления Пуассона выполнены.