Курсовая работа: Контрольные карты Шухарта в системе управления качеством

Серия длиной в семь точек рассматривается как ненормальная. Кроме того, ситуацию следует рассматривать как ненормальную, если:

а) не менее 10 из 11 точек оказываются по одну сторону от центральной линии;

б) не менее 12 из 14 точек оказываются по одну сторону от центральной линии;

в) не менее 16 из 20 точек оказываются по одну сторону от центральной линии.

3. тренд – непрерывно повышающаяся или понижающаяся кривая.

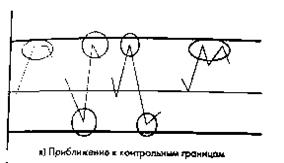
4. приближение к контрольным границам. Если 2 или 3 точки оказываются очень близки к контрольным границам, это свидетельствует о ненормальности распределения.

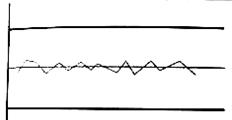
5. приближение к центральной линии. Если значения концентрируются около центральной линии, это может свидетельствовать о неверном выборе способа группировки, что делает размах слишком широким и приводит к смешиванию данных различным распределений.

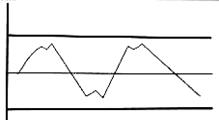
6. периодичность. Когда, спустя, определенные равные промежутки времени, кривая идет то на «спад», то на «подъем».

VII. Анализ контрольных карт.

Дальнейшие действия основываются на выводе о стабильности или нестабильности процесса. Если процесс не отвечает критериям стабильности, следует уменьшить влияние неслучайных факторов и, собрав новые данные, построить контрольную карту. Но, если процесс отвечает критериям стабильности, необходимо оценить возможности процесса (Cp). Чем меньше разброс параметров внутри границ допуска, тем выше значение показателя возможности процесса. Показатель отражает отношение ширины параметра и степень его разброса. [9] Индекс возможности рассчитывается как , где можно вычислить как .

Если вычисленный показатель меньше 1, то исследователю нужно усовершенствовать процесс, либо остановить изготовление продукции, либо изменить требования к продукции. При значении индекса:

Cр<1 возможности процесса неприемлемы,

Cр=1 процесс находится на грани требуемых возможностей,

Cр>1 процесс удовлетворяет критерию возможности.

В случае отсутствия смещения относительно центральной линии Cp=Cpk, где . Два этих показателя используют всегда совместно, для определения статуса процесса, так, в машиностроении считается нормой , что означает, что вероятность несоответствия не превышает 0,00006.

Дальше, следует скорректировать процесс на полученные данные и проводить его регулярный (постоянный) мониторинг с помощью контрольных карт.

Теперь, рассмотрев алгоритм построения контрольных карт, разберем конкретный пример.

Задание: Контролируется содержание хрома в стальных отливках. Проводят замеры в четырех плавках. В таблице 2 приведены данные по 15 подгруппам. Необходимо построить карту.

Решение: Поскольку уже заранее известно, какой тип карты необходимо построить, вычислим значения

номер подгруппы	X1	X2	X3	X4		R
1	0,74	0,76	0,62	0,73	0,713	0,14
2	0,72	0,74	0,84	0,69	0,748	0,15
3	0,87	0,79	0,70	0,92	0,820	0,22
4	0,78	0,66	0,71	0,74	0,723	0,12
5	0,81	0,66	0,82	0,67	0,740	0,16
6	0,63	0,71	0,68	0,82	0,710	0,19
7	0,63	0,73	0,64	0,80	0,700	0,17
8	0,66	0,68	0,85	0,91	0,775	0,25
9	0,63	0,66	0,62	0,85	0,690	0,23
10	0,85	0,61	0,75	0,77	0,745	0,24
11	0,73	0,65	0,74	0,90	0,755	0,25
12	0,85	0,77	0,65	0,69	0,740	0,20
13	0,67	0,69	0,83	0,62	0,703	0,21
14	0,74	0,73	0,62	0,88	0,743	0,26
15	0,81	0,82	0,69	0,73	0,763	0,13
средние:	0,738	0,19

Следующим шагом будет вычисление , где, в соответствии с вышеуказанной схемой, , а . Теперь, имея, значения центральной линии, среднего значения показателя и среднего отклонения, найдем значения контрольных границ карт .

Для значений нижние и верхние контрольные границы определяются по формулам: