Курсовая работа: Корреляционный анализ солнечной и геомагнитной активностей

Обычная стрелка компаса уравновешивается, вращаясь горизонтально на вертикальной оси. Компасная стрелка, уравновешенная до намагничиванию и способная вращаться в плоскости магнитного меридиана вокруг горизонтальной оси, называется буссолью наклонения, или инклинатором. В северной полусфере Земли почти везде северный полюс магнитной стрелки направлен вниз (I положительно), в южном полушарии вниз направлен южный полюс стрелки (I отрицательно). Области положительного и отрицательного I разделены линией (называемой магнитным экватором, или экватором наклонения), вдоль которой I= 0. Магнитная стрелка (уравновешенная до намагничивания) в любой точке на этой кривой располагается горизонтально.

В точках, где горизонтальная компонента В исчезает, магнитная стрелка устанавливается вертикально. Эти точки называются полюсами магнитного наклонения, или полюсами наклонения. Две основные точки такого типа обычно называются магнитными полюсами Земли. Одна из них находится в Арктике, вторая – в Антарктиде. На эпоху 1965г. их координаты были соответственно 75°,6 с.ш., 101° з.д. и 66°,3 ю.ш., 141° в.д.

В любой точке Р на сферической поверхности имеется естественное направление, характеризующее эту точку, — радиальное направление. Поскольку Н, Z и I определяются относительно этого направления, а В вообще не требует для своего определения какого-либо направления, эти четыре составляющие можно назвать собственными магнитными элементами. Но В не может быть определено полностью только этими элементами. Чтобы определить азимут Н, нужно выбрать некоторое нулевое направление, от которого можно отсчитать магнитное склонение D. В качестве такого направления выбрано направление на северный географический полюс. Так как ось вращения Земли не связана непосредственно с конфигурацией геомагнитного поля, D (как и X, Y) определяется относительно условного направления, принятого на основе простого соглашения. Поэтому D, X и Y можно назвать относительными магнитными элементами.

4. Индексы, характеризующие геомагнитные вариации

1) Локальный К-индекс – квазилогарифмический индекс (увеличивается на 1 при увеличении возмущённости ≈ в 2 раза), вычисляемый по данным конкретной обсерватории за 3-х часовой интервал времени. Таким образом, мы имеем 8 К-индексов для каждых гринвичских суток. Для одного интервала используются магнитограммы для трёх компонентов (, D —магнитное склонение, т.е. угол между плоскостями гринвичского и магнитного меридианов; Н —магнитный меридиан, азимут которого определяется по D; Z —показатель напряженности магнитного поля по вертикали, см. рис.10) на каждой станции. Для каждой компоненты оценивается амплитуда r в течении интервала учитывается поправка на вариации солнечно-суточные (Sq), лунно-суточные (L), а когда необходимо, вариации радиационного излучения (Sqа). (Sqа исключаются, т.к. они обусловлены рентгеновским и ультрафиолетовыми излучениями из областей солнечных вспышек, а не потоком солнечной плазмы.)

Наибольшая из трёх амплитуд в каждом временном интервале. используется для К-индекса. Для каждой обсерватории имеется таблица, дающая пределы r, определяемое полулогафмической шкалой, для каждой из 10 величин К. Например, таблица.1 для обсерваторий на широте 50°.

Таблица 1.

r(g)	0 ô 5ô 10ô 20ô 40ô 70 ô 120 ô 200ô 300 ô>500ô
K	0 1 2 3 4 5 6 7 8 9

2) Трёхчасовой планетарный К_р - индекс, введенный Бартельсом в 1939г., усреднённые К–индексы для 12 выбранных обсерваторий, расположенных в северном и южном полушариях, от умеренных широт вплоть до 63°(изменяется от 0 до9).

Таблица 2.

Обсерватория	Широта	Обсерватория	Широта
Минук (Канада)	61,8°N	Руде Сков (Дания)	55,9°N
Ситка (Аляска)	60,0	Вингст (Ирландия)	51,6
Лервик (Шотландия)	62,5	Виттевин (Голландия)	54,1
Эксдалемьюр (Шотландия)	58,5	Хартланд (Англия)	54,6
Лёво (Швеция)	58,1	Ажинкоурт (Канада)	55,1
Фредериксбург (США)	49,6	Амберлей (Новая Зеландия)	47,7°S

К_р – индекс отражает флуктуации электрического тока, не учитывая структуру поля возмущения. Интерпретация связи между К_р – индексом и другими геомагнитными данными не всегда прямая. Одна из причин заключается в том, что 12 станций, участвующих в определении К_р – индекса, расположены в субавроральной зоне. Это указывает на то, что большие значения Кр, как 6, 7, 8, 9, обусловленные главным образом полярными магнитными возмущениями. С другой стороны, низкие значения К_р могут быть следствиями других типов геомагнитных возмущений.

Количественно состояние магнитного поля в зависимости от К_р можно приблизительно охарактеризовать данным образом

Таблица 3.

Кр £=2 и менее	спокойное
Кр = 2 …3	слабо возмущенное
Кр = 4	возмущенное
Кр = 5 …6	магнитная буря
Кр ³= 7 и более	большая магнитная буря

К_р - индекс обладает полулогарифмической связью с амплитудой r . Для того, чтобы К_р перевести в линейную шкалу Бартельс ввел следующую таблицу для получения трехчасового ар – индекса, измеряющего изменчивость индукции (индуктивность) геомагнитного поля в нанотесла (нТл),

Таблица 4.

Кр	= 00 0+ 1- 10 1+ 2- 20 2+ 3- 30 3 4- 40 4+
ар	= 0 2 3 4 5 6 7 9 12 15 18 22 27 32
Кр	= 5- 50 5+ 6-60 6+ 7- 70 7+ 8- 80 8+ 9-90
ар	= 39 48 56 67 80 94 111 132 154 179 207 236 300 400

Эта таблица составлена таким образом, что ар – индекс станций на геомагнитной широте ~ 50° может рассматриваться как амплитуда наиболее возмущенной из трех компонентов поля, выражаемая в единицах 2g. Ежедневный Ар –индекс получается в результате суммирования восьми величин ар для каждого дня. Именно он использован в данной работе.

5. Постановка задачи

Цель работы :

Статистический анализ Ар и Rw- индексов, описывающих солнечную и геомагнитную активности, c помощью их автокорреляционных и взаимокорреляционной функций.

Вычитая из функции Х(t) ее среднее значение по 365 точкам, приводим исходную реализацию к виду Y(t), близкой к стационарному в смысле математического ожидания. Очевидно, что это ожидание центрирует реализацию, т.е. m_y (t) = 0.

Систематика оценок: оценки характеристик случайных функций обознацим символом «тильда», K(t) – оценка приближенного значения корреляционной функции, полученного по реализации конечной длины.

Оценка параметра несмещённая, если при увеличении объема выработки и ее реализации математическое ожидание оценки стремится к истинному значению параметра, т.е. оценка не имеет систематической ошибки, оценка параметра состоятельна, если при увеличении длины реализации дисперсия оценки стремится к нулю. Несмещенная оценка является эффективной, если она обладает свойством минимума дисперсии по сравнению с другими оценками. В предположении эргодичности изучаемого процесса в качестве оценки корреляционной функции можно принять следующее выражение:

где (1)

Из-за конечности реализации, что предполагает y(t) = 0 при t < 0 и t > T , при вычислении K_х ( t ) при конкретном t верхний предел интеграла и нормированный множитель превращаются T- t , т.е.

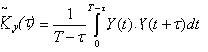(2)

При равномерном дискретном задании реализации интервал между отдельными t равен T/n, n—общее число измеренных значений. Тогда t = m·∆t = m·T /n , T- t =( n – m) T /n, а выражение (2) превращается в

(3)

Эта оценка корреляционной функции является несмещенной, но, к сожалению, несостоятельной. Последнее утверждение чего понять, если учесть, что при m → n в формировании оценки принимает участие всего несколько сомножителей, из-за чего дисперсия оценки (3) не будет стремиться при больших m к нулю каким бы большим не было число n. По этой причине подобная оценка обычно используется при m £n /5/

Чтобы получить состоятельную оценку корреляционной функции, приходится вводить весовую функцию, которую часто называют окном данных. Смысл подобного преобразования заключается в уменьшении веса значений корреляционной функции при больших m пропорционально числу точек, принимающих участие в формировании этих значений.

Простейший вид весовой функции – это «треугольник»