Курсовая работа: Критерій Байєса-Лапласа при експоненційно розподілених даних для множини оптимальних рішень

Експоненціальний розподіл:

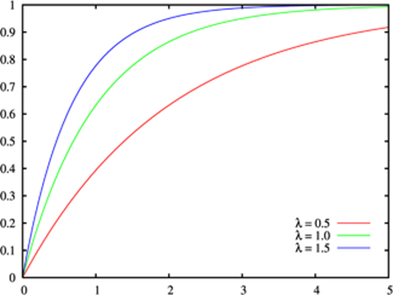
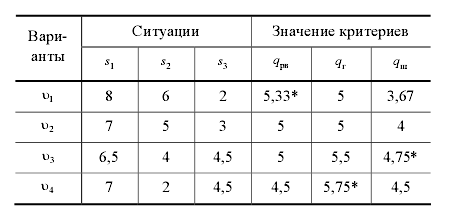
Рисунок 1 – Графік експоненціального закону розподілу

Цьому закону розподілу підлягає багато явищ, наприклад тривалість телефонних розмов, строк служби електронних деталей, час прибуття літака в аеропорт та ін. [4]

Розділ 2. Математичний опис

Приклад №1:

Розглянемо задачу ПР із 6 альтернативами із 8 можливими станами.

Задано матриці U(х,s) – станів і р(х,s) – ймовірностей, значення яких подані в таблиці 1 і таблиці 2 відповідно:

Таблиця 1 – Значення матриці U(х,s)

s1	s2	sЗ	s4	s5	s6	s7	s8
х1	1	2	-2	0	4	6	7	-4
х2	0	0	-1	0	5	6	1	2
хЗ	4	1	1	2	1	0	2	З
х4	-6	7	5	5	2	2	0	З
Х5	-1	-1	0	4	2	З	4	5
х6	-2	-1	-2	2	1	0	З	4

Таблиця 2 – Значення матриці р(х,s)

s1	s2	sЗ	s4	s5	s6	s7	s8
х1	0	0	0	0.5	0	0.5	0	0
х2	0	0	0	0	0.2	0	0	0.8
хЗ	0.1	0.2	0	0	0	0	0	0.7
х4	0	0	0	1	0	0	0	0
Х5	1	0	0	0	0	0	0	0
х6	0	0.4	0	0	0.6	0	0	0

Тоді за методом Байєса – Лапласа – хопт є шукаємо множину оптимальних рішень:

Отже, хопт є {х4}.

Приклад №2:

Початковими даними для прийняття рішення служить матриця ефективностей,

,

тут - ефективність варіанта,

в ситуации

.

Матриця ефективностей:

Таблиця 3 – Початкові дані для прийняття рішень