Курсовая работа: Квантование сигналов по времени

Дискретизация по времени заключается в замене непрерывного по времени сигнала X(t) дискретным сигналом, значения которого для дискретных моментов времени t совпадают соответственно с мгновенными значениями непрерывного сигнала. Такая операция называется также квантованием сигнала по времени.

Дискретизация по уровню (квантование по уровню) заключается в замене непрерывного множества значений сигнала X(t) множеством дискретных значений. При этом шкала возможных значений сигнала разбивается на определенное количество интервалов и непрерывное значение сигнала заменяется ближайшим дискретным. Полученные дискретные значения затем кодируются (обычно двоичным кодом).

КИМ (кодо-импульсная модуляция) обеспечивает существенное повышение помехоустойчивости передачи сообщений. Кроме того, дискретизация по времени позволяет использовать одни и те же устройства (каналы связи, устройства обработки информации и пр.) для большого числа различных сигналов.

При КИМ весьма важным является правильный выбор способа квантования сигнала по времени и уровню. В связи с этим рассмотрим некоторые вопросы теории квантования непрерывных функций по времени и уровню.

3. Квантование сигналов по времени

3.1 Определение дискретизации сигналов по времени

При квантовании по времени непрерывная по аргументу функция x(t) преобразуется в функцию дискретного аргумента. Такое преобразование может быть выполнено путем взятия отсчетов функции x(t) в определенные дискретные моменты времени . В результате функция x(t) заменяется совокупностью мгновенных значений x(ti) [i=0,1,2,…,n].

Временной интервал между двумя соседними фиксированными моментами времени, в которых задается дискретная функция, называется интервалом временного квантования. Величина, обратная интервалу временного квантованияназывается частотой квантования.

Частота квантования должна выбираться таким образом, чтобы по отсчетным значениям x(ti) можно было бы с заданной точностью получить исходную функцию.

3.2 Выбор шага квантования по времени

Известно несколько критериев выбора частоты квантования по времени. К таким критериям относится, в частности, частотный критерий В.А. Котельникова. Данный критерий, который получил название теоремы В.А. Котельникова, основывается на следующей модели сигналов:

сигнал представляет собой стационарный случайный процесс;

спектр сигнала сплошной и ограничен некоторой частотой, за пределами которой он тождественно равен нулю.

Теорема В.А. Котельникова: если непрерывная функция x(t) удовлетворяет условиям Дирихле (ограничена, кусочно-непрерывная и имеет конечное число экстремумов) и ее спектр ограничен некоторой частотой fc, то она полностью определяется отсчетами, находящимися на расстоянии друг от друга.

Для доказательства теоремы рассмотрим выражения прямого и обратного преобразования Фурье непрерывной функции x(t).

(1)

. (2)

В рассматриваемом частном случае функции с ограниченным спектром можно записать

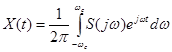. (3)

Дополним функцию до периодической с периодом, равным 2fc (рисунок 1) и разложим ее в ряд Фурье

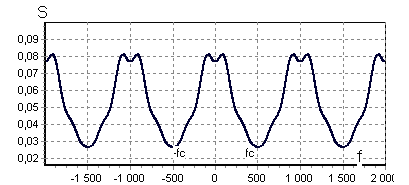
Рисунок 1 - функция с периодом, равным 2fc.

, (4)

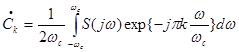. (5)

Сравнивая выражения (3) и (5) замечаем, что они совпадают с точностью до постоянного множителя , если принять .

Следовательно,

.

Подставив найденное выражение для в (4), получим

. (6)

После подставки (6) в (3), замены знака при k (т.к. суммирование производится по всем положительным и отрицательным значениям k) и перестановки операций суммирования и интегрирования получим

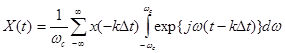. (7)

Вычислим интеграл