Курсовая работа: Квантование сигналов по времени
т.к. 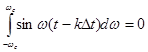 .
.
После подстановки (8) в (7) окончательно получим
![]() . (9)
. (9)
Полученное выражение представляет аналитически теорему Котельникова.
Из (9) видно, что непрерывная функция X(t) (рисунок 2, а), обладающая ограниченным спектром, может быть представлена разложением в ряд, каждый член которого выражается одинаковой функцией вида sin(x)/x (функция отсчета), но с различными коэффициентами ![]() (рисунок 2, б).
(рисунок 2, б).
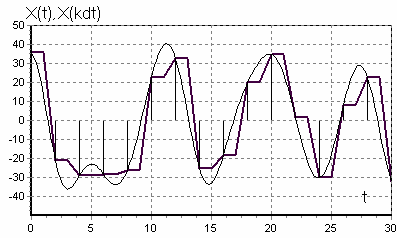
Рисунок 2, а - Функция отсчета
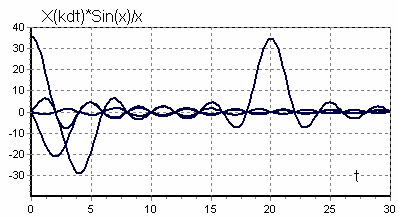
Рисунок 2, б - Функция отсчета, но с различными коэффициентами ![]()
Ряд (9) представляет собой разложение случайного процесса с координатными функциями (детерминированными функциями времени) и весовыми коэффициентами ![]() , являющимися случайными величинами, равными мгновенным значениям сигнала в точках
, являющимися случайными величинами, равными мгновенным значениям сигнала в точках ![]() .
.
Функция отсчетов в момент времени ![]() достигает максимума и равна единице. В моменты времени
достигает максимума и равна единице. В моменты времени ![]() , где i=1,2,3… функция отсчетов убывает, обращаясь в нуль при t=∞.
, где i=1,2,3… функция отсчетов убывает, обращаясь в нуль при t=∞.
Сумма (9) в каждый k-ый момент времени определяется только одним k‑ым слагаемым, т.к. все остальные слагаемые в этот момент времени обращается в нуль. Внутри промежутка ![]() восстанавливаемая функция определяется всеми слагаемыми (рисунок 21, а - непрерывная плавная линия).
восстанавливаемая функция определяется всеми слагаемыми (рисунок 21, а - непрерывная плавная линия).
3.3 Воспроизведение непрерывного сигнала
Известно, что функция вида ![]() представляет собой реакцию идеального фильтра нижних частот с граничной частотой
представляет собой реакцию идеального фильтра нижних частот с граничной частотой ![]() на дельта-функцию. Следовательно, если в приемном устройстве поместить такой фильтр и пропустить через него квантованный сигнал, представляющий собой последовательность с частотой
на дельта-функцию. Следовательно, если в приемном устройстве поместить такой фильтр и пропустить через него квантованный сигнал, представляющий собой последовательность с частотой ![]() весьма кратковременных импульсов, амплитуды которых пропорциональны отсчетам исходной непрерывной функции, то, суммируя выходные сигналы фильтра, можно воспроизвести с достаточно высокой степенью точности исходный непрерывный сигнал.
весьма кратковременных импульсов, амплитуды которых пропорциональны отсчетам исходной непрерывной функции, то, суммируя выходные сигналы фильтра, можно воспроизвести с достаточно высокой степенью точности исходный непрерывный сигнал.
Однако нас интересует случай, когда сигнал x(t) ограничен во времени (Tc). В этом случае сумма (9) будет конечной
![]() , (10)
, (10)
где ![]() .
.
Усечение бесконечной суммы, т.е. ограничение ее теми значениями Xk, которые оказываются в пределах Tc, уменьшает точность представления сигнала x(t).
Это первый фактор, определяющий точность представления.
Кроме того, сигнал конечной длительности имеет бесконечный спектр гармонических составляющих. Поэтому ограничение спектра сигнала некоторой частотой ![]() является вторым фактором, снижающим точность представления непрерывного сигнала x(t) дискретными отсчетами.
является вторым фактором, снижающим точность представления непрерывного сигнала x(t) дискретными отсчетами.
Средний квадрат относительной погрешности в этом случае определяется выражением
![]() ,
,
где Е – полная энергия неограниченного спектра сигнала;
![]() - энергия «хвоста» спектра, т.е. той его части, которая расположена за пределами fc .
- энергия «хвоста» спектра, т.е. той его части, которая расположена за пределами fc .
Чтобы погрешность формулы (10) была мала, должно выполняться условие
![]() . (11)
. (11)
Дополнительная погрешность вносится при восстановлении сигнала x(t) за счет не идеальности фильтра нижних частот, т.к. идеальный фильтр НЧ физически нереализуем (предполагает наличие отклика на ![]() -функцию при t<0, т.е. до начала подачи на вход).
-функцию при t<0, т.е. до начала подачи на вход).
Однако на практике никогда не требуется идеально точное воспроизведение передаваемого сигнала, поэтому ограничивают спектр сигнала диапазоном с верхней частотой ![]() , в котором сосредоточена основная энергия сигнала.
, в котором сосредоточена основная энергия сигнала.
Дисперсия приведенной погрешности, возникающей в результате усечения, будет
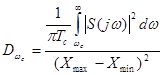 ,
,