Курсовая работа: Линейка из рупорных антенн

,

.

Рис. 6. Диаграмма направленности синфазной антенны

Ширину диаграммы направленности антенны по нулевому уровню и по уровню 0,5 определим следующим образом [3]:

,

.

Уровень боковых лепестков:

.

Положение первого дифракционного максимума определим по формуле:

φ_диф = ± arcsin(p·λ / d),

где р – номер дифракционного лепестка.

φ_диф = ± arcsin(3,1 / 20) = ±8,9^о .

Диаграмма направленности линейки излучателей в Н - плоскости будет такой же, как и у одного излучателя в Н – плоскости.

2. Несинфазный режим работы.

Рассчитаем максимальное отклонение ДН антенны от нормали к ее поверхности:

φ_max = φ_0,7изл .

По графику ДН одиночного рупора в плоскости Е (рис. 3) определяем, что φ_max = 4^о .

Расстояние между излучателями решетки с электрическим качанием луча должно быть меньше оптимального [3]. В нашем случае размер раскрыва рупора в плоскости, в которой происходит отклонение луча, равен оптимальному значению. Таким образом, уменьшить расстояние между излучателями невозможно, а значит, дифракционные лепестки множителя решетки будут входить в основной лепесток ДН излучателя. Это приведет к росту боковых лепестков ДН антенны.

Разность фаз токов излучателей ∆ψ найдем из формулы, определяющей направление максимального излучения[3].

,

,

.

Диаграмму направленности антенны в несинфазном режиме найдем перемножением диаграммы одного излучателя в Е-плоскости F₂ (θ₂ ) на множитель решетки F_n (θ₂ ) при ∆ψ = 2,8 рад.

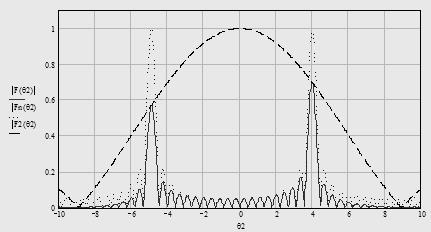
Рис. 7. Диаграмма направленности антенны в несинфазном режиме работы

Рассчитаем коэффициент направленного действия и коэффициент усиления антенны.