Курсовая работа: Лінійна залежність n мірних векторів Програма

Вступ

Теорія

Опис програми

Текст програми

Контрольні приклади

Висновки

Література

Вступ

Дана робота присвячена введенню, одного з найважливіших понять, яке використовується не тільки в алгебрі, але й в багатьох інших розділах математики. Дамо просте визначенню лінійної залежності системи векторів в мірному просторі.

Визначення (*) Система векторів називається лінійно залежної, якщо існує такий набір коефіцієнтів , з яких хоча б один відмінний від нуля, що .

Система векторів, що не є лінійно залежної, називається лінійно незалежної. Але останнє визначення краще сформулювати по іншому.

Визначення (**) Система векторів називається лінійно незалежної, якщо рівність можлива тільки при .

Теорія

Припущення 1 Система векторів лінійно залежний тоді і тільки тоді, коли один з векторів системи є лінійною комбінацією інших векторів цієї системи.

Доведення .

Нехай система векторів лінійно залежна. Тоді існує такий набір коефіцієнтів , що , причому хоча б один коефіцієнт відмінний від нуля. Припустимо, що . Тоді:

,

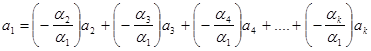тобто є лінійною комбінацією інших векторів системи.

Нехай один з векторів системи є лінійною комбінацією інших векторів. Припустимо, що це вектор , тобто . Очевидно, що . Одержали, що лінійна комбінація векторів системи дорівнює нулю, причому один з коефіцієнтів відмінний від нуля (дорівнює ).

Припущення 2 Якщо система векторів містить лінійно залежну підсистему, те вся система лінійно залежна.

Доведення.

Нехай у системі векторів підсистема , , є лінійно залежної, тобто ,, і хоча б один коефіцієнт відмінний від нуля. Тоді складемо лінійну комбінацію ,. Очевидно, що ця лінійна комбінація дорівнює нулю, і що серед коефіцієнтів є ненульовий.

Припущення 3 Система, що складається з одного вектора, лінійно залежна тоді і тільки тоді, коли цей вектор нульової.

Доведення .

Нехай система складається з вектора . Лінійна комбінація має вид . Якщо , то , тобто система лінійно залежна. Якщо і , то .

Припущення 4 Система, що складається з двох векторів, лінійно залежна тоді і тільки тоді, коли ці вектори колінеарні.

Доведення цієї пропозиції тривіальне – воно аналогічно доказу наступного припущення.

Припущення 5 Система з трьох векторів лінійно залежна тоді і тільки тоді, коли ці вектори компланарні.

Доведення .

Нехай вектори - компланарні. Якщо - колінеарні, то в силу попереднього пропозиції вони утворять лінійно залежну підсистему системи . За припущенням 2 система - лінійно залежна. Якщо вектори - не колінеарні, то є лінійною комбінацією векторів і за припущенням 1 система векторів - лінійно залежна.

Нехай система векторів лінійно залежна. За припущенням 1 один вектор, скажемо , є лінійною комбінацією інших векторів, і , . Права частина останньої рівності лежить у площині, у якій лежать вектори . Тому вектор лежить в одній площині з векторами , тобто вектори - компланарні.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--