Курсовая работа: ЛИСП-реализация операций над матрицами

Невозможно вычислить разность матриц, так как число строк матрицы A не равно числу строк матрицы B..

Транспонирование матрицы A и B:

Так как матрица A не квадратная невозможно выполнить ее транспонирование.

.

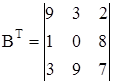Умножение матрицы A на число 5:

.

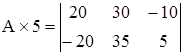Умножение матриц :

.

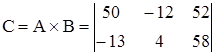2 Математические и алгоритмические основы решения задачи

2.1 Сумма матриц

Суммой двух матриц А и В одинаковых размеров называется матрица того же размера, элементы которой равны сумме соответствующих элементов матриц А и В. Таким образом, если

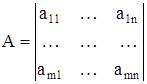(1)

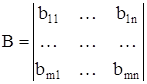(2)

.

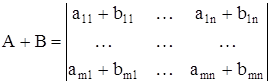Операция нахождения суммы матриц называется сложением матриц и распространяется на случай конечного числа матриц одинаковы размеров.

2.2 Разность матриц

Так же, как и сумма, определяется разность двух матриц

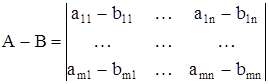
Операция нахождения разности двух матриц называется вычитанием матриц. Проверкой можно убедиться, что операция сложения матриц удовлетворяет следующим свойствам:

А + В = В + А; (коммутативность)

А + (В + С) = (А + В) + С; (ассоциативность)

А + О = А.

Здесь А, В, С – произвольные матрицы одинаковых размеров; О – нулевая матрица того же размера.

2.3 Умножение матрицы на число λ

Произведением матрицы А = [аij] на число λ называется матрица, элементы которой получаются из соответствующих элементов матрицы А умножением их на число λ. Произведение обозначим λА. Таким образом от умножения матрицы (1) на число, получим:

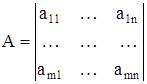, то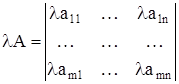

Проверкой можно убедиться, что операция умножения матрицы на число удовлетворяет следующим свойствам:

1) А = А;

2) (λ + μ)А = λА + μΑ;