Курсовая работа: ЛИСП-реализация операций над матрицами
Содержание
Введение........................................................................................................... 2
1 Постановка задачи....................................................................................... 4
2 Математические и алгоритмические основы решения задачи................... 7
2.1 Сумма матриц............................................................................................ 7
2.2 Разность матриц........................................................................................ 7
2.3 Умножение матрицы на число λ............................................................... 8
2.4 Умножение матриц.................................................................................... 9
2.5 Транспонирование матрицы................................................................... 10
3 Функциональные модели и блок-схемы решения задачи......................... 12
4 Программная реализация решения задачи............................................... 18
5 Пример выполнения программы............................................................... 27
Заключение.................................................................................................... 29
Список использованных источников и литературы.................................... 30
Введение
Многие теоретические и практические вопросы приводят не к одному уравнению, а к целой системе уравнений с несколькими неизвестными. Особенно важен случай системы линейных уравнений, т.е. системы m уравнений 1ой степени с n неизвестными:
![]() a11x1 + … + a1n xn = b1 ;
a11x1 + … + a1n xn = b1 ;
a21x1 + … + a2n xn = b2 ;
………………………………
am1x1+ … + amnxn = bm .
Здесь x1, … , xn – неизвестные, а коэффициенты записаны так, что индексы при них указывают на номер уравнения и номер неизвестного. Значение систем 1ой степени определяется не только тем, что они простейшие. На практике часто имеют дело с заведомо малыми величинами, старшими степенями которых можно пренебречь, так что уравнения с такими величинами сводятся в первом приближении к линейным. Не менее важно, что решение систем линейных уравнений составляет существенную часть при численном решении разнообразных прикладных задач. Ещё Г.Лейбниц (1693) обратил внимание на то, что при изучении систем линейных уравнений наиболее существенной является таблица, состоящая из коэффициентов, и показал, как из этих коэффициентов (в случае m = n) строить так называемые определители, при помощи которых исследуются системы линейных уравнений. Впоследствии такие матрицы, или матрицы, стали предметом самостоятельного изучения, так как обнаружилось, что их роль не исчерпывается приложениями к теории систем линейных уравнений. Современная алгебра, понимаемая как учение об операциях над любыми математическими объектами, является одним из разделов математики, формирующих общие понятия и методы для всей математики. Для современной алгебры характерно то, что в центре внимания оказываются свойства операций, а не объектов, над которыми проводятся данные операции. Классическим разделом алгебры является линейная алгебра, т.е. теория векторных пространств и модулей, частью которых являются сформировавшиеся ещё в XIX веке теория линейных уравнений и теория матриц. Идеи и методы линейной алгебры применяются во многих разделах математики. Так, основным предметом изучения функционального анализа являются бесконечномерные векторные пространства.
1 Постановка задачи
Требуется разработать программу, реализующую основные операции алгебры матриц: сложение, вычитание, умножение, транспонирование, а также умножение матрицы на число.
Пример 1. Над матрицами А и В выполнить основные операции:

 .
.
Сумма матриц:
 .
.
Разность матриц:
 .
.
Транспонирование матрицы A и B:

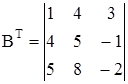 .
.
Умножение матрицы A на число 3:
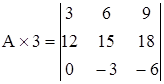 .
.
Умножение матриц ![]() :
:
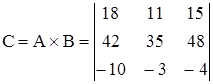
Пример 2. Над матрицами А и В выполнить основные операции:
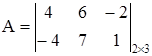
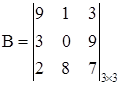 .
.
Сумма матриц:
Невозможно вычислить сумму матриц, так как число строк матрицы A не равно числу строк матрицы B.
--> ЧИТАТЬ ПОЛНОСТЬЮ <--