Курсовая работа: ЛИСП-реализация операций над матрицами

4) λ( μА) = (λμ)А;

5) А + (-А) = О.

Здесь А, В – произвольные матрицы; μ, λ - произвольные числа; О – нулевая матрица.

2.4 Умножение матриц

Произведение АВ матрицы А на матрицу В определяется только в том случае, когда число столбцов матрицы А равно числу строк матрицы В. Пусть матрицы А и В такие, что число столбцов матрицы А равно числу строк матрицы В:

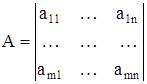
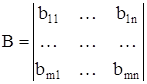
В этом случае произведением матрицы А на матрицу В, которые заданы в определенном порядке (А – 1ая, В – 2ая), является матрица С, элемент которой сij определяется по следующему правилу:

cij = ai1b1j + ai2b2j + … + ainbnj = ∑ n α = 1 aiαbαj,

где i = 1,2, …, m; j = 1, 2, …, k.

Для получения элемента сij матрицы произведения С = АВ нужно элементы i-й строки матрицы А умножить на соответствующие элементы j-го столбца матрицы В и полученные произведения сложить.

Число строк матрицы С = АВ равно числу строк матрицы А, а число столбцов – числу столбцов матрицы В.

Умножение матриц некоммутативно, т.е.

АВ ≠ ВА.

Проверкой можно показать, что умножение матриц удовлетворяет следующим свойствам:

1) А(ВС) = (АВ)С; (ассоциативность);

2) λ(АВ) = (λА)В = А(λВ);

3) А(В + С) = АВ + АС. (дистрибутивность).

Здесь А, В, С – матрицы соответствующих определению умножения матриц размеров; λ - произвольное число.

Операция умножения двух прямоугольных матриц распространяется на случай, когда число столбцов в 1ом множителе равно числу строк во 2ом, в остальных случаях произведение не определяется. А также, если матрицы А и В – квадратные одного и того же порядка, то умножение матриц всегда выполнимо при любом порядке следования сомножителей.

2.5 Транспонирование матрицы

Транспонированием матрицы называется такое преобразование матрицы, при котором строки и столбцы меняются ролями при сохранении номеров. Транспонированная матрица обозначается АТ.

.

Для квадратной матрицы это преобразование эквивалентно симметричному отображению относительно главной диагонали.

3 Функциональные модели и блок-схемы решения задачи

Функциональные модели и блок-схемы решения задачи представлены на рисунках 1 – 7.

Условные обозначения:

MATRIX1 – первая матрица;

MATRIX2 – вторая матрица;