Курсовая работа: Механика вертолета

Получили уравнение:

. (2.6)

Составляем характеристическое уравнение:

; .

Частное решение имеет вид:

. (2.7)

Определим константы и , для чего найдем :

;

Подставив и в уравнение (2.6):

;

;

получим:

. (2.8)

Окончательно имеем:

;

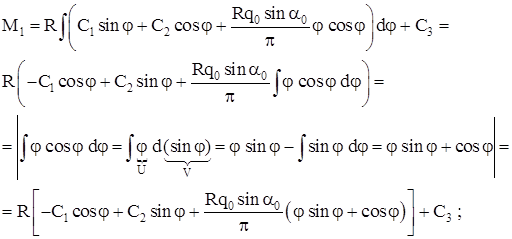
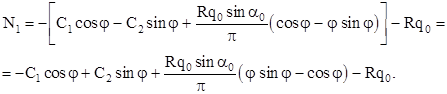
Для второй системы дифференциальных уравнений решение проводится аналогично.

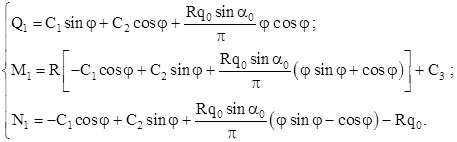(2.9)

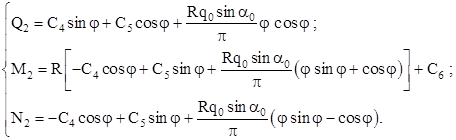(2.10)

Для определения неизвестных констант интегрирования воспользуемся граничными условиями и условиями сопряжения участков кольца:

при : 1) ;

при : 2) ;

при : 3) ; (2.11)

4) ;

5) .

Первые два условия из (2.11) справедливы, так как при симметричном нагружении кососимметричные факторы на оси симметрии равны нулю.