Курсовая работа: Метод простой итерации для решения систем линейных алгебраических уравнений

Время счета для второго способа: 1.32

Число операций при решении вторым способом: 9333

Приложение 3

График итерационного процесса на примере решения системы (4.1) с x ^{( 0 )} =(1000,1000,1000) программой METOD 1

График итерационного процесса на примере решения системы (4.1) с x ^{( 0 )} =(1000,1000,1000) программой METOD 2

График итерационного процесса на примере решения системы (4.1)

с x ^{( 0 )} =(1,1,1) программой METOD 1

График итерационного процесса на примере решения системы (4.1) с x ^{( 0 )} =(1,1,1) программой METOD 2

График итерационного процесса на примере решения системы (4.2)

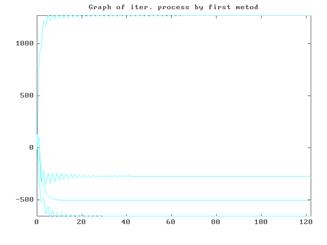с x ^{( 0 )} =(0,10,20,30) программой METOD 1
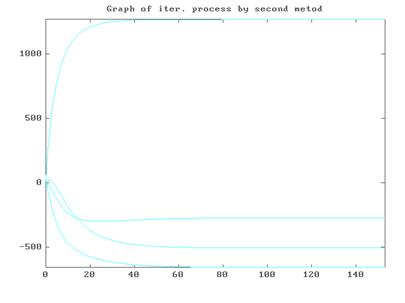График итерационного процесса на примере решения системы (4.2) с x ^{( 0 )} =(0,10,20,30) программой METOD 2

График итерационного процесса на примере решения системы (4.2)

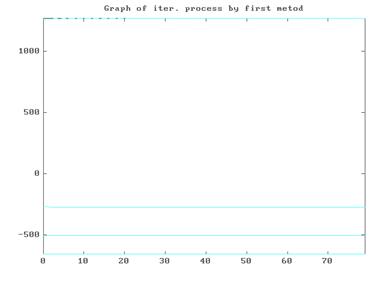с x ^{( 0 )} =(-270,-503,1260,-653) программой METOD 1

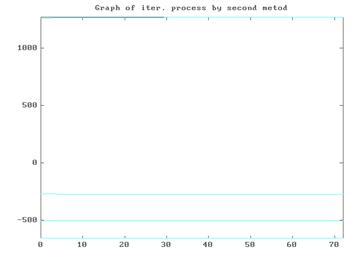
График итерационного процесса на примере решения системы (4.2) с x ^{( 0 )} =( -270,-503,1260,-653) программой METOD 2

Графики зависимостей погрешностей решений системы (4.1) от шага итерации при использовании программы METOD 1. M и при x ^{( 0}

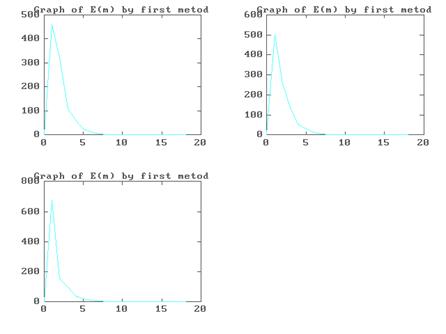⁾ =(1000,1000,1000)
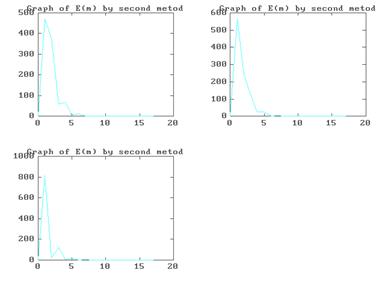Графики зависимостей погрешностей решений системы (4.1) от шага итерации при использовании программы METOD 2. M и при x ^{( 0 )} =(1000,1000,1000)

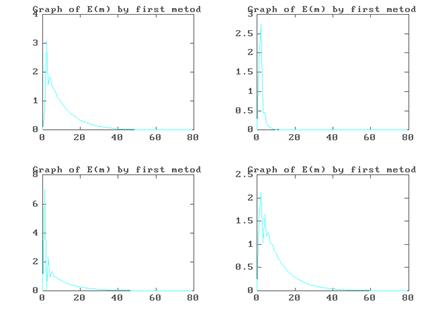
Графики зависимостей погрешностей решений системы (4.1) от шага итерации при использовании программы METOD 1. M и при x ^{( 0}

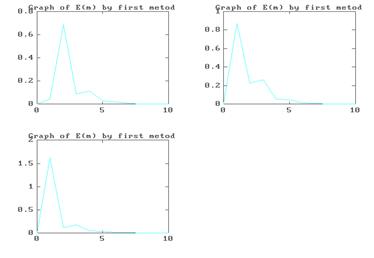⁾ =(1,1,1)

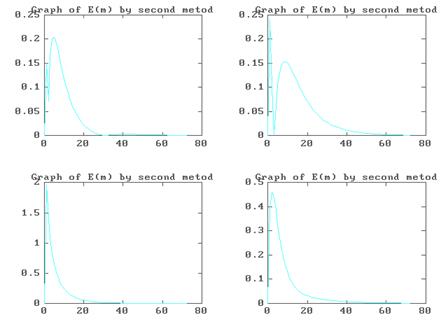
Графики зависимостей погрешностей решений системы (4.1) от шага итерации при использовании программы METOD 2. M и при x ^{( 0 )} =(1,1,1)

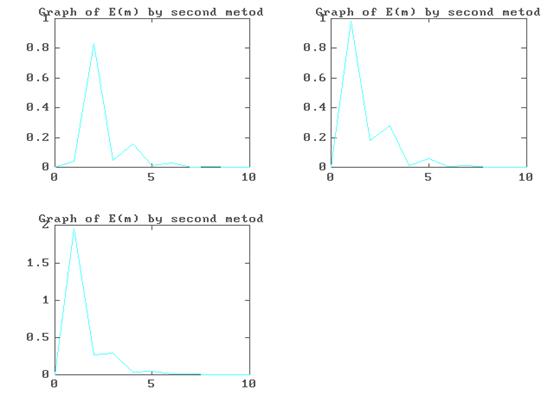
Графики зависимостей погрешностей решений системы (4.2) от шага итерации при использовании программы METOD 1. M и при x ^{( 0 )} =(-

270,-503,1260,-653)
Графики зависимостей погрешностей решений системы (4.2) от шага итерации при использовании программы METOD 2. M и при x ^{( 0 )} =(-270,-503,1260,-653)

Графики зависимостей погрешностей решений системы (4.2) от шага итерации при использовании программы METOD 1. M и при x ^{( 0}

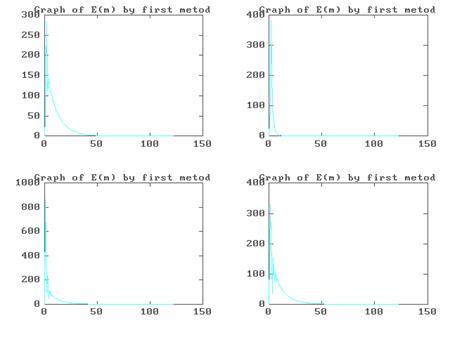⁾ =(0,10,20,30)
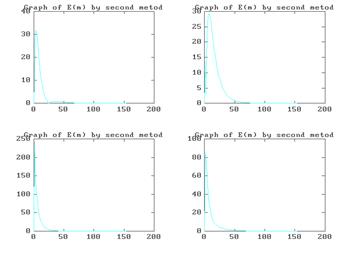Графики зависимостей погрешностей решений системы (4.2) от шага итерации при использовании программы METOD 2. M и при x ^{( 0 )} =(0,10,20,30)

Список литературы

1. Копченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах.- М.: Наука, 1972

2. Крылов В.И., Бобков В.В., Монастырский П.И. Вычислительные методы.- М.: Наука, 1976

3. Сарычева О.М. Численные методы в экономике.- Новосибирск, 1995