Курсовая работа: Метод релаксации переменных решения СЛАУ

(1.7)

Если точность не достигнута, то выполняется следующая итерация. В системе (1.5) заменяем на и находим значения . После этого вновь проверяем, достигнута точность решения или нет.

Заметим, что в некоторых особых случаях может иметь место сходимость итерационного процесса к некоторым значениям, которые не являются решением задачи. В этом случае, по-видимому, предпочтительнее в качестве критерия сходимости использовать невязку, получаемую при подстановке найденного решения в исходную систему.

Запишем выражение i +1- итерации черезi :

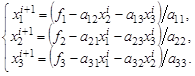(1.8)

Если точность решения достигнута, то счет прекращается.

Для систем m -го порядка имеем

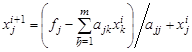(1.9)

Запишем метод простых итераций в матричной форме. Представим матрицу А в виде суммы трех матриц

А=А 1 +D +A 2 ,

(1.10)

где D = diag[a ₁₁ , a ₂₂ , ..., a _mm ] - диагональная матрица,

А ₁ = 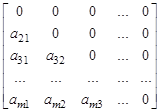- нижняя треугольная матрица,

А ₂ = 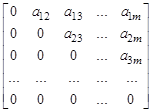- верхняя треугольная матрица.

Представим систему (1.1) в матричной форме

(1.11)

Метод Якоби в матричной записи выглядит следующим образом

,

(1.12)

Или

, .

(1.13)

Существуют итерационные методы, обладающие лучшей скоростью сходимости, чем методы Якоби. В этих методах при вычислении i +1 итерации компоненты вектора решения используются, найденные на i + 1 итерации компоненты решения с номерами , l =1,2,...,j -1. Наиболее распространенным методом подобного типа является метод Зейделя. Продемонстрируем его применение на системе (1.3). Вновь, задавая начальное приближение, для первой итерации запишем

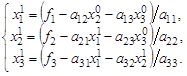(1.14)

После проверки условия сходимости совершаем вторую итерацию и т.д. Для i + 1 итерации запишем

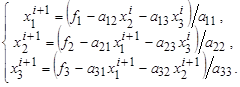(15)

Общая формула имеет вид

.

(1.16)

Запишем метод Зейделя в матричной форме

,

(1.17)

или в форме близкой к каноническому виду

,	(1.18)
.	(1.19)

Äëÿ îäíîøàãîâûõ èòåðàöèîííûõ ìåòîäîâ, ñóùåñòâóåò êàíîíè÷åñêàÿ ôîðìà çàïèñè

.

(1.20)

Здесь - матрица, задающая тот или иной итерационный метод, - итерационный параметр. В случае метода Якоби - это матрица D , а =1, в случае метода Зейделя =D +А ₁ , а итерационный параметр также равен единице =1.

Формируя матрицу B различным образом и задавая различные значения итерационного параметра, можно получать одношаговые итерационные методы самого разного вида. В зависимости от выбора этих параметров мы будем получать методы, которые будут обладать различной скоростью сходимости, т.е. заданная точность будет достигаться за разное число итераций.

Одним из наиболее распространенных одношаговых итерационных методов является метод верхних релаксаций^* , который имеет следующий вид

,

(1.21)