Курсовая работа: Метод векторів та його застосування

Теорема 1 . ( перша ознака рівності двох векторів).

Для того щоб два вектори були рівними, необхідно і достатньо, щоб вони були однаково напрямленими і мали рівні довжини.

Доведення:

1. Необхідність. Нехай вектори і рівні. Доведемо, що і =.

Якщо =, то, за означенням 1, множини напрямлених відрізків, які відповідають цим векторам, збігаються. Тому , =. Звідси ,=, що й треба було довести.

2. Достатність. Нехай , =. Доведемо, що =. Якщо, , =, то , =, тобто і належать одній і тій же множині однаково напрямлених відрізків рівної довжини. А це означає, що =. Теорему доведено.

Наслідок. Два вектори, кожен з яких дорівнює третьому, рівні між собою.

Теорема 2. (теорема про відкладання вектора).

Від будь-якої точки простору можна відкласти вектор, рівний даному, і до того ж єдиний.

Доведення: Нехай даний вектор зображається напрямленим відрізком . Виберемо у просторі довільну точку О , сполучимо точку В з точкою О і позначимо середину відрізка ОВ через С (мал. 3). Проведемо

відрізок АС і відкладемо на його продовженні відрізок CM =АС . Чотирикутник АВМО є паралелограмом, бо його діагоналі точкою перетину діляться пополам. Звідси випливає, що промені АВ і ОМ однаково напрямлені, а відрізки АВ і ОМ рівні. Отже, ==.

Доведемо тепер, що цей вектор єдиний. Припустимо, що існує інший вектор =, відмінний від . Але ж і =, тому =. Отже, , =, тому точки M і збігаються, що суперечить припущенню. Тобто від точки O можна відкласти лише один вектор, рівний даному вектору . Теорему доведено.

Означення 2. Два вектори називаються протилежними, якщо вони протилежно напрямлені і мають рівні довжини. Вектор, протилежний до , позначається - (мал. 4). Очевидно, =-, – (-)=.

Додавання векторів, властивості операції додавання векторів

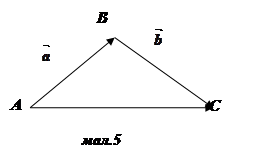
Введемо операцію додавання векторів, яка відіграє важливу роль в векторній алгебрі.

Означення. Нехай задано два вектори і . Від деякої точки A відкладемо вектор =, потім від точки B відкладемо вектор =. Вектор = називається сумою векторів і і позначається так: =+ (мал. 5). Помітимо, що для знаходження двох неколінеарних векторів доводиться будувати трикутник. Тому вказане правило додавання векторів називають правилом трикутника. Це правило можна сформулювати так: для будь-яких трьох точок A , B і C +=, або: сумою векторів і євектор , який сполучає початок вектора з кінцем вектора при умові, що вектор відкладено від кінця вектора .

З цього правила випливає правило паралелограма : якщо вектори і відкладені від спільного початку O , =, = (мал. 6) і на них побудовано паралелограм OACB , то сумою векторів + є вектор =, який виходить з того ж початку і збігається з діагоналлю OC паралелограма.

Розглянемо властивості операції додавання векторів.

Властивість 1 . Операція додавання векторів комутативна , тобто для будь-яких векторів і : +=+.

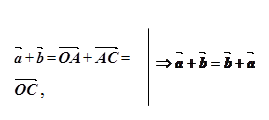Доведення: За правилом трикутника маємо (мал. 7):

Властивість 2. Операція додавання векторів асоціативна , тобто для будь-яких векторів , , : (+)+= +(+)

Доведення: Візьмемо довільну точку A і від неї відкладемо вектори =, =, = (мал. 8). Тоді +=, (+)+=; +=; +(+)=. Отже, (+)+ =+(+).

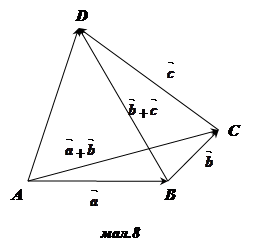
Властивість 3. Сумою протилежних векторів є нуль-вектор: +(-)=0.

Доведення. Нехай =, тоді -=, і за правилом трикутника матимемо +(-)=+==0.