Курсовая работа: Метод золотого перерізу для пошуку екстремумів функцій

і відомо значення Нехай уже визначено точки , локалізований відрізок , обчислено відповідні значення функції

.У цьому випадку

,

Відома точка , яка виконує золотий переріз відрізка , і обчислено значення мінімізаційної функції в цій точці: За іншу точку вибираємо , яка є другою точкою золотого перерізу відрізка

У цій точці обчислюємо і визначаємо локалізований відрізок , а саме (будемо вважати, що ) у випадку приймемо , а у випадку (випадок розглядається аналогічно). Новий відрізок є локалізований

Точка - це точка золотого поділу відрізка і в цій точці обчислено значення функції Якщо кількість обчислень функції не обмежено,то цей процес можна продовжити доти, доки не виконається нерівність - задана точність обчислень. Якщо кількість обчислень функції задана і дорівнює n , то після отримання локалізованого відрізка обчислення припиняємо і на розв’язок задачі другого типу беремо - наближення до множини з похибкою

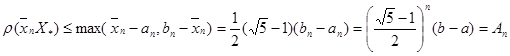
Якщо враховувати аналогічну оцінку в методі поділу відрізка наполовину

Отже, навіть для малих n метод золотого поділу ефективніший, ніж метод поділу відрізка наполовину. Недоліком методу золотого поділу в запропоновану вигляді є його нестійкість. Розглянемо числову реалізації методу. Обов’язково число буде задано наближено, а це призведе до наближеного обчислення точок Розглянемо як ця похибка впливатиме на результат наступних кроків. Уведемо позначення тоді маємо різницеве рівняння з початковими умовами (2)

Розв’язок шукатимемо у вигляді для визначення маємо характеристичне рівняння (3)

Лінійно незалежними частинними розв’язками рівняння (2) будуть , де - корені рівняння (3) . Довільний розв’язок (2) можна записати у вигляді

(4)

Сталі С₁ ,С₂ можна визначити з початкових умов

(5)

У разі точного розв’язування системи (5)

тоді Однак на практиці замість у системі (5) беремо наближене значення і замість (4) з точними значеннями С₁ ,С₂ = 0 отримаємо

Оскільки то похибка становитиме

і зі збільшенням n зростатиме досить швидко. Отже, уже для малих n точки відрізнятимуться від теоретичних, які можна отримати лише внаслідок точних обчислень. Практичні підрахунки також підтвердили нестійкість методу. Цей недолік можна легко усунути. Нехай маємо локалізований відрізок і внутрішню точку із обчисленим значенням . Знаходимо точки золотого поділу відрізка

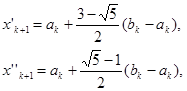
Точку, яка є далі від точки вибираємо за В іншому алгоритм незмінний. За такої модифікації метод втрачає симетричність і красу в обчисленні, однак зберігає стійкість і повністю відповідає теоретичним висновкам.

2. Постановка задачі

Задача 1. Знайти для заданої функції і заданого відрізка .