Курсовая работа: Методические особенности введения показательной функции в курсе математики средней школы

4 урок – закрепление изученного материала по теме «Показательная функция».

Ознакомление учащихся с показательной функцией начиная с изучения свойств степеней.

Курс алгебры знакомит учащихся с понятием степени с рациональным показателем. Таким образом для любого основания степени (где , ). Можно построить функцию: , , область определения которой – множество действительных чисел, необходимо ввести определение, степени с иррациональным показателем. Используемое свойство степени с основным, например, большим единицы (возрастании), рациональное приближение иррационального числа α: r₁ < α< r₂ . Исходя из графического изображения зависимости показателя степени и значения степени, показывается, что найдется такое значение y, которое будет наибольшим среди всех a^{r 1} и наименьшим среди всех a^{r 2} , которое можно считать значением a^α .

Затем формируется определение показательной функции: функция, заданная формулой y=a^x (, ), называется показательной функцией с основанием a, и формулируемые основные свойства: D(a^x )=R; E(a^x )=R_Т ; a^x возрастает при a>1 и a^x убывает при 0<a<1; напоминаются основные свойства степеней. Т.о. показательная функция есть систематизация, обобщение и расширение знаний учащихся о свойствах степени.

В качестве приложения свойств показательной функции рассматриваются решения простейших показательных уравнений и неравенств.

Функция – новый математический объект для учащихся.

1. Область определения показательной функции множество действительных чисел.

2. Область значений показательной функции множество действительных чисел.

3. При а>1 функция возрастает на всей числовой прямой.

4. При 0<а<1 функция убывает на всей числовой прямой.

5. При любых действительных х и у справедливо равенство а х *ау=аху.

6. Область значения функции у=3х+1 числовой промежуток (-4; 4).

7. Область определения показательной функции у=а х промежуток (-4; 4).

8. Функция у=0,2 х убывает на R.

9. Функция у=0,7х возрастает на R.

10. График функции у=2 х проходит через точку (0; 1).

2.3 Методические особенности изучения степенной функции

Степень с рациональным показателем является наиболее важным этапом изучения степенной функции , где x>0, α, и наиболее трудным для восприятия материалом в школьном курсе алгебры.

Подходы к изучению степенной функции в науке и в школьном курсе математике различны. Существуют различные способы определения степенной функции; наиболее распространенное и наиболее общее из них – аксиоматическое.

Определение . Степенной функцией называется любой непрерывный гамоморфизм группы R в себя, то есть любая функция f, отображающая множество в себя, обладающая свойствами:

1) для всех x, y

2) – непрерывна.

Для некоторых значений α степенная функция допускает продолжение на более широкую область определения, чем . Например, при на , кроме этого ; если же , где , то только на .

При α>0 можно доказать, что lim=0 при , поэтому, чтобы не нарушалась непрерывность функции , и в этомслучае полагают, что .

При нечетном и функция допускает естественное продолжение на всю числовую прямую; при четном n – это невозможно.

Равенство 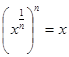по сути задает функцию как функцию, обратную функции , поэтому функцию , например, можно считать определенной для всех , а функцию только для неотрицательных .

В общем виде на не накладывается никакие условия, поэтому функция считается определенной на множестве .

При изучении степенной функции в школьном курсе математики подходят совсем с других позиций: постепенно расширяются значения числа , причем рассматриваются не функции, например, , , а вводится понятие степени определенного вида.

Получаем следующую последовательность: степень с натуральным показателем (7 класс) – степень с нулевым и целым отрицательным показателем (7 класс) – степень с рациональным нецелым показателем (11 класс) – степень с иррациональным показателем (11 класс).