Курсовая работа: Методика изучения квантовой оптики в базовой и профильной школах

Важно при этом подчеркнуть, что наблюдают прямую пропорциональность, а не равенство, так как часть падающих на металл фотонов отражается, а из поглощенных фотонов не все вырывают из металла свободные электроны. Энергия части поглощенных фотонов превращается во внутреннюю энергию металла. Поэтому отношение числа электронов n к числу падающих на металл фотонов n _ф значительно меньше единицы (для чистых металлов примерно в 1000 раз).

Далее объясняют, почему наибольшая кинетическая энергия фотоэлектронов зависит от частоты падающего света, а не от его интенсивности (второй закон фотоэффекта). Из уравнения Эйнштейна следует:

Так как для данного вещества работа выхода постоянна (А =const), то наибольшая кинетическая энергия фотоэлектронов пропорциональна частоте падающего света. Анализируют случай, когда энергия светового кванта равна работе выхода А :

или

Следовательно, вся энергия фотона идет на совершение работы выхода и скорость электронов равна нулю. Минимальная (граничная) частота фотоэффекта v ₀ равна А/ h , а максимальная длина волны . При условии v < v ₀ и λ> λ₀ фотоэффекта нет. Это длинноволновая (красная) граница фотоэффекта. Ее значение зависит только от работы выхода, т. е. от химической природы металла, и может лежать на любом участке оптического диапазона. Для каждого вещества есть определенная длинноволновая граница фотоэффекта (третий закон фотоэффекта).

Таким образом, уравнение Эйнштейна объясняет все законы внешнего фотоэффекта. Оно позволяет вычислять скорости фотоэлектронов и определять наибольшую длину волны, при которой еще наблюдается явление фотоэффекта для данного вещества, а также вычислить работу выхода для конкретного металла.

После анализа уравнения Эйнштейна можно показать, как была осуществлена экспериментальная проверка этого уравнения. Она состояла в определении постоянной Планка из результатов опыта.

Так как работа выхода для данного вещества — величина постоянная, то кинетическая энергия фотоэлектрона является линейной функцией частоты излучения, падающего на фотоэлемент. Точка В соответствует граничной частоте фотоэффекта, а отрезок ОС — работе выхода А . Измерив задерживающее напряжение и определив работу выхода (зная граничную частоту для данного металла), можно по этим данным найти постоянную Планка

, ,

откуда

, .

Таким образом, тангенс угла наклона прямой к оси частот равен постоянной Планка, т. е.

Для всех металлов этот угол одинаков.

При практическом проведении таких измерений встретились большие трудности. Первые тщательные измерения постоянной Планка этим методом были выполнены в 1915 г. Р. Милликеном. Он получил значение, близкое к тому, какое было уже известно из теории теплового излучения.

В нашей стране в 1928 г. опытами П. И. Лукирского и С. С. Прилежаева была подтверждена линейная зависимость кинетической энергии фотоэлектронов от частоты падающего света и получено значение постоянной Планка.

Для закрепления уравнения Эйнштейна решают задачи на вычисление скорости и энергии электронов, красной границы фотоэффекта, работы выхода.

Рис. 5

3.2. ЭФФЕКТ КОМПТОНА

Формирование представлений о фотоне, начатое при изучении: фотоэффекта, продолжают при изучении последующих вопросов курса - эффекта Комптона, давления света, химического действия света.

Особенно важное значение для доказательства квантовых свойств света имеет впервые введенное в программу физики общеобразовательной средней школы понятие об эффекте Комптона. До этого данное явление, являющееся решающим подтверждением наличия у фотона импульса, изучалось только на факультативном курсе и в классах с углубленным изучением физики.

Комптоновский эффект заключается в изменении частоты излучения при рассеянии рентгеновских лучей "легкими" веществами (графит, парафин и др.). Особенность этих веществ - относительно слабая связь внешних электронов в атоме с ядрами. Это явление было обнаружено в 1923 г. и подробно исследовано американским физиком А. Комптоном, который установил, что разность частот (длин волн) первичного (падающего) и рассеянного излучения зависит только от угла рассеяния.

Интересно отметить, что именно А. Комптон назвал кванты света фотонами. В дальнейшем А. Комптон и независимо П. Дебай теоретически объяснили явления с квантовых позиций, рассматривая рассеяние как результат взаимодействия рентгеновских квантов падающего излучения с практически свободными электронами вещества, применяя к этому процессу законы сохранения энергии и импульса. Полученная зависимость:

,

где m ₀ –масса частицы, на которой происходит рассеяние, прекрасно согласовывалась с экспериментальными данными.

Формулу для изменения длины волны комптоновского рассеяния в школьном курсе не дают, но подходы к ее выводу на основании рассмотрения законов сохранения (энергии и импульса) для системы электрон - фотон можно привести.

Порядок рассуждений может быть примерно следующим.

Объяснить наблюдаемое различие частот первичного и рассеянного излучений с волновых позиций не представляется возможным. Действительно, механизм рассеяния рентгеновского излучения согласно волновой теории света можно объяснить только за счет возникновения вторичных электромагнитных волн в результате вынужденных колебаний ("раскачивания") электронов в атомах вещества под действием электрического поля первичной волны. При этом частота рассеянного излучения должна совпадать с частотой первичного излучения.

Если считать поток рентгеновских лучей состоящим из отдельных фотонов, летящих со скоростью света и способных испытывать столкновения с другими частицами, то следует допустить возможность обмена с ними энергией и импульсом.

Рентгеновский фотон с частотой ν обладает энергией , массой , импульсом . Энергия электрона до столкновения m ₀ c ² (где m ₀ – масса покоя электрона, так как электрон до столкновения считают неподвижным в данной системе отсчета).

При столкновении фотона с электроном происходит передача энергии и импульса фотона этому электрону. Электрон приобретает кинетическую энергию. Энергия испущенного в результате столкновения фотона меньше начальной, что приводит к уменьшению его частоты.

При элементарном акте рассеяния должен выполняться закон сохранения энергии и закон сохранения импульса (для системы фотон - электрон, которую можно считать изолированной):

;

,

где m ₀ c ² – полная энергия неподвижного электрона, m c ² – полная энергия электрона после столкновения с фотоном, – энергия первичного фотона, – энергия фотона после столкновения с электроном (рассеянного фотона), и - импульсы первичного и рассеянного фотонов; - импульс электрона после столкновения с фотоном (, , ).

Совместное решение этих уравнений, выполненное на основе представлений о фотоне как частице, способной испытывать столкновения с электроном по законам релятивистской механики, т. е. с учетом того, что электрон после столкновения приобретает скорость, близкую к скорости света, и его массу рассчитывают по формуле:

,
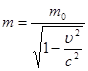