Курсовая работа: Методика вивчення тригонометричних функцій у старшій школі з використанням мультимедійних засобів

Радіанну міру кутів широко використовують у математиці, фізиці, техніці. Передумовою її запровадження був такий факт: якщо розглянути два концентричні кола радіусів і (Рис. 2.1) і два різні центральні кути  і  з відповідними дугами і , і , то за відомою формулою довжини дуги

, , , .

Поділивши обидві частини кожної з чотирьох рівностей на відповідний радіус, дістанемо:

, , , .

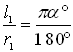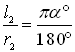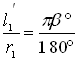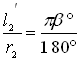Звідси

, .

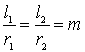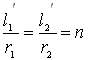Якщо , то . Отже, для деякого центрального кута відношення довжин дуг концентричних кіл до радіусів є величиною сталою і може слугувати характеристикою величини відповідного центрального кута. Встановлено, що для довільного центрального кута , де – стала для цього центрального кута. Число а, що дорівнює відношенню довжини дуги до радіуса кола, називають радіанною мірою кута.

Якщо , то а=1. Тому в радіанній системі за одиницю виміру величини кута взято центральний кут, для якого довжина відповідної дуги дорівнює довжині радіуса. Міру цього кута називають радіаном. Радіан є одиницею радіанної міри кутів. Радіанною мірою дуги кола називають радіанну міру відповідного центрального кута.

Для радіанної міри кута і відповідної одиниці традиційно не запроваджено позначення. Тому якщо розглядають тригонометричну функцію кута, міра якого виражена в градусах, наприклад , то записують . Якщо міра кута виражена в радіанах, то пишуть

. Це означає, що цей кут містить радіан, а у виразі sin 2—2 радіани.

Деякі учні помилково вважають, що символ є позначенням одиниці радіанної міри. Щоб спростувати це неправильне уявлення, потрібно у прикладах використовувати аргументи тригонометричних функцій не тільки з ірраціональним числом або його частками, а й з іншими дійсними числами.

Специфікою радіанної міри є й те, що радіан міститься в розгорнутому куті =3,14 разів, а градус 180. Перевага радіанної системи вимірювання кутів – формули довжини дуги і площі сектора у випадку вимірювання відповідного центрального кута в радіанах спрощуються: , де – радіус кола, а – радіанна міра центрального кута. (Порівняйте з формулами

, ).

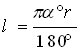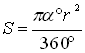Найбільшою перевагою радіанної міри – для малих кутів, виміряних у радіанах, виконуються наближені рівності , . Справді, нехай =3°. Оскільки 3°=0,0524 радіана, а sin 3°=0,0523, то справедлива наближена рівність sin 0,0524=0,0523. Для градусної міри рівність sin3°=3 не має смислу. Цю властивість радіанної міри широко застосовують у математичному аналізі та інших науках.

Практика свідчить, що виведення формул переходу від градусної міри кута до радіанної і навпаки не спричинює труднощів в учнів. Помилок вони припускаються, здебільшого заокруглюючи наближені значення, отримані під час застосування згаданих формул.

2.2 Введення поняття тригонометричних функцій числового аргументу

Насамперед потрібно згадати означення тригонометричних функцій кута і поширити їх на будь-яку градусну міру, ввести кут повороту. Крім того, слід переконати учнів, що існує відповідність між множиною дійсних чисел і множиною точок одиничного кола, для чого попередньо виконати таку вправу.

Приклад 1. Позначити на одиничному колі точки , в які відображується початкова т.Р0(1;0) при повороті навколо центра кола на кут радіанів, якщо , , , , , (Рис.2.2).

Розв'язання. За із формули довжини дуги, вираженої через радіанну міру, випливає , де – радіанна міра центрального кута і відповідної йому дуги. Це означає, що числове значення довжини дуги збігається з числовим значенням її радіанної міри.

Оскільки т., в яку відображається т.Р0(1;0), лежить на перетині осі у з колом і , , то т., в яку відображається Р0(1;0), лежатиме на колі між точками і . Точки і містяться на колі в 4-й чверті симетрично точкам і відносно осі .

Числу відповідає точка початок Р0 (1;0) – початок відліку дуг на одиничному колі, числу – т., яка є кінцем дуги, що дорівнює двом дугам .

Розв'язуючи цю вправу, небажано переходити від радіанної міри до градусної, хоч учням легше замінити 1 рад на 57°, а рад – на 90° і відшукати т. на дузі кола. Важливо навчити учнів знаходити відповідні точки на колі для кутів, заданих радіанною мірою, оскільки метою є ввести поняття тригонометричної функції довільного числа.

На завершення розв'язування цієї вправи доцільно розглянути координатну вісь, яка є дотичною до одиничного кола в т.Р0(1;0), має початком відліку цю точку й одиницю відліку, що дорівнює радіусу одиничного кола. Якщо намотувати цю координатну вісь на одиничне коло, то наочно виявляється відповідність між множиною R дійсних чисел і множиною точок одиничного кола.

Увагу учнів звертають на те, що кожній т. на одиничному колі відповідають її абсциса й ордината, які також залежать від числа . Тому маємо ще дві залежності між дійсним числом і абсцисою та ординатою відповідної т., в яку відображується початкова т.Р0(1;0) одиничного кола при повороті навколо центра кола на кут радіанів. Отже, існують відповідності між множиною дійсних чисел і множиною абсцис і ординат т. одиничного кола. Ці залежності (відповідності) дістали назву тригонометричних функцій числа або тригонометричних функцій числового аргументу.

Означення 1. Синусом числа називають ординату точки одиничного кола, в яку переходить початкова точка Р0(1;0) при повороті навколо центра кола на кут радіанів. Його позначають .

Означення 2. Косинусом числа називають абсцису точки одиничного кола, в яку переходить початкова точка Р0(1;0) при

повороті навколо центра кола на кут радіанів. Його позначають .

Означення 3. Тангенсом числа називають відношення , а котангенсом числа – відношення , їх позначають відповідно , .