Курсовая работа: Методологічні основи статистики
Побудова багатофакторних індексних моделей, що відображають результативний показник як добуток взаємодії складових його факторів, має ґрунтуватися на знанні певних принципів, що випливають з об'єктивних особливостей взаємозв'язку між явищами.
Метод комплексних статистичних коефіцієнтів може бути успішно використаний для оцінки результатів господарської діяльності фірм, підприємств і організацій, показників соціально-економічного розвитку регіонів, країн у світі, виконання планів виробництва асортименту продукції, рівномірності її постачання, для оцінки стійкості курсу валют, акцій, цінних паперів та ефективності їх купівлі та продажу.
Основними методами для кількісної оцінки взаємозв'язків економічних явищ є регресійний і кореляційний аналіз.
Перед розглядом передумов кореляційного і регресійного аналізу слід сказати, що загальною умовою, що дозволяє отримати стабільніші результати при побудові кореляційних і регресійних моделей, є вимога однорідності початкової інформації. Ця інформація повинна бути оброблена на предмет аномальних, тобто що різко виділяються з масиву даних, спостережень. Ця процедура виконується за рахунок кількісної оцінки однорідності сукупності за яким-небудь одновимірним або багатовимірним критерієм (залежно від початкової інформації) і має на меті відбір тих об'єктів спостереження, у яких якнайкращі (або найгірші) умови функціонування з незалежних або слабозалежних причин.
Після обробки даних на предмет "аномальності" слід провести перевірку, наскільки інформація, що залишилася, задовольняє передумовам для використання статистичного апарату при побудові моделей, оскільки навіть незначні відступи від цих передумов часто зводять до нуля отримуваний ефект. Треба зауважити, що імовірнісне або статистичне рішення будь-якої економічної задачі повинне ґрунтуватися на докладному осмисленні початкових математичних понять і передумов, коректності і об'єктивності збору початкової інформації, в постійному поєднанні економічного змісту і математико-статистичного аналізу.
Застосування регресійного і кореляційного аналізу вимагає чіткого дотримання таких критеріїв, як наявність численної сукупності об'єктів, нормального розподілу змінних, кореляційної залежності тощо. Нормальний розподіл сукупності простежується тільки у випадках дії багатьох незалежних або слабозалежних чинників та відсутності значимих показників. Зокрема, як стверджують І. М. Григор'єва та М. С. Кузнєцов, "...досліджувана сукупність має бути у кращому разі у 7 разів більша від кількості коефіцієнтів регресії" .
Модель регресії може будуватися на припущенні, що на якусь залежну змінну впливає лише один фактор, тоді регресія називається простою, однак практика доводить різноманіття взаємозв'язків між явищами і процесами (особливо в макроекономічній сфері), тобто на залежну змінну впливає значна кількість чинників, а тому для опису таких моделей застосовуються множинні регресії.
Побудова багатофакторної (множинної) кореляційно-регресійної моделі включає такі етапи:
1. Вивчення економічної проблеми та підготовка статистичних даних.
У відповідності до визначеної мети дослідження, яке проводиться, необхідно з'ясувати природу процесів, які потрібно буде описувати. Для цього необхідно дати чітке визначення економічних явищ, встановлення об'єктів та періодів дослідження. На цьому етапі повинні бути сформульовані припущення про залежність досліджуваних явищ.
2. Побудова статистично значущих моделей.
Цей етап полягає у тому, щоб за допомогою спеціальних характеристик отримати кількісне підтвердження наявності чи відсутності зв'язку між показниками. При оцінюванні взаємозв'язку між кількісними змінними підтвердження гіпотези про наявність зв'язку є основою для переходу до наступного кроку — встановлення аналітичної залежності між ознаками. Вид аналітичної залежності або конкретної формули, який встановлює взаємну відповідність між ознаками, обирається виходячи зі змістовного аналізу явища. Якщо про характер взаємозв'язку попередньо нічого не відомо, то в процесі дослідження перевіряються різні гіпотези, випробовуються різні формули з відбором за формальними критеріями тієї з них, яка найбільш правдоподібна і більшою мірою відповідає наявним фактичним даним про значення ознак, про окремі об'єкти сукупності. Після вибору форми аналітичного зв'язку результативної та факторних ознак постає завдання визначення конкретних числових значень параметр.
Параметри рівняння регресії розраховуються таким чином, щоб обчислені за рівнянням значення залежної ознаки найменшою мірою відрізнялися від фактичних. Це досягається розрахунком параметрів рівнянь регресії за методом найменших квадратів (МНК). Параметри регресії за даним методом обираються таким чином, щоб забезпечити мінімальну суму квадратів відхилень фактичних величин від обчислених за рівнянням регресії для заданих значень факторних ознак .
3. Перевірка адекватності моделей та вибір найкращої моделі з усіх статистично значущих.
Рішення про вибір, рівень якості теоретичної моделі та надійність статистичних висновків у регресійному аналізі визначається рівнем статистичних оцінок адекватності моделі реальним явищам і процесам.
Для багатомірної регресійної моделі важливим є також оцінка наявності мультиколінеарності, тобто високого рівня парної кореляції залежності факторних ознак, які викривляють форму зв'язку факторних ознак і результативної. Єдиної, загальноприйнятої оцінки мультиколінеарності поки що не існує, але найбільш розповсюдженою є оцінка мультиколінеарності за значенням коефіцієнтів парної кореляції для факторних ознак.
І нарешті, в множинній регресії поруч з оцінкою достовірності моделі в цілому може іти мова про оцінювання достовірності кожного параметра моделі. Ця мета досягається за допомогою і-критерію Ст'юдента. Коефіцієнт регресії вважається досить надійним, якщо фактичне значення і-критерію перевищує табличне. Якщо надійність коефіцієнта регресії не підтверджується, то робиться висновок про несуттєвість у моделі факторної ознаки і необхідності її вилучення з моделі або заміни.
4. Економічна інтерпретація.
Результати регресійного аналізу порівнюються з гіпотезами, які були сформульовані на першому етапі досліджень, і оцінюється їх правдоподібність з економічної точки зору.
Спираючись на теоретичні положення, спробуємо продемонструвати практичне використання кореляційно-регресійного аналізу при побудові моделі взаємозв'язку між темпами економічного зростання та обсягом людського капіталу. Як впливовий фактор розглядатимемо частку загальної кількості тих, хто навчався (з урахуванням освіти у вищих закладах та професіонально-технічних навчальних закладах), у населенні України. Зв'язок між темпом економічного зростання та часткою тих, хто навчався, в населенні України у 1993— 2006 рр.1 подано на рис. 1.
Як бачимо, зв'язок є прямим. Такий результат цілком узгоджується з ідеєю загального позитивного впливу освітнього рівня на економічне зростання. А щільність зв'язку (Я2 = 0,45) є суттєвою, тож можна зробити висновок, що частка тих, хто навчався, у населенні країни є впливовим фактором щодо темпів економічного зростання.
Знання сутності методу і його можливостей щодо оцінювання інформації дає змогу ефективно використовувати статистичні методи для аналізу взаємозв'язків між економічними явищами. Ці методи втрачають інтерес у практичній роботі аналітика, коли немає впевненості в їх відповідності при вирішенні конкретних завдань.
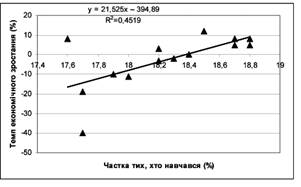
Рис.1. Зв'язок між темпом економічного зростання та часткою тих, хто навчався
Вивчення причинно-наслідкових зв'язків здійснюють шляхом застосування статистичних методів у такій послідовності: статистичне групування; індексний аналіз; дисперсійний аналіз; кореляційно-регресійний аналіз; методи багатомірного статистичного аналізу (метод головних компонент, кластерний аналіз, факторний аналіз). Одержані результати розрахунків перевіряють на вірогідність за відповідними критеріями надійності. Порядок і послідовність комплексного підходу у статистико-економічному дослідженні схематично наведено на рис. 1.
6. Застосування статистичних методів на практиці
Потрібно відзначити, що в економічних розрахунках аналітичного напрямку майже зовсім не використовується досить ефективний спосіб математико-статистичної обробки даних - дисперсійний метод аналізу. Як і інші ймовірнісно-статистичні методи, він набагато розширює можливості економістів в аналізі виробництва й ефективності прийняття управлінських рішень. За його допомогою розв'язуються наступні аналітичні завдання: кількісне вимірювання сили впливу факторних ознак та їх сполучень на результативну; вивчення вірогідності впливу та його довірчих меж; аналіз окремих середніх та статистична оцінка їх різниць. У поглибленому економічному аналізі дисперсійний метод може виконувати допоміжні функції. У цьому плані його використання відкриває широкі можливості щодо науково-обґрунтованого підходу застосування інших статистичних методів кількісного аналізу.
Наведені нижче розрахунки щодо кількісного виміру впливу факторів ефективного використання земель сільськогосподарськими підприємствами послугують прикладом практичного застосування статистичних оцінок в аналітичній роботі.
Оскільки доцільність збільшення обсягів матеріальних, грошових і трудових вкладень у виробництво повинно корелювати з підвищенням показників економічної ефективності використання землі, зазначену залежність легко встановити шляхом побудови комбінаційних статистичних групувань (табл. 1).