Курсовая работа: Методы анализа основной тенденции (тренда) в рядах динамики

Темпы роста, выраженные в коэффициентах, принято называть коэффициентами роста:

.

Темп роста представляет всегда положительное число.

3. Темп прироста или темп сокращения (темп изменения уровней) показывает, на сколько процентов уровень данного периода больше или меньше определенного уровня, характеризует относительную скорость изменения уровня ряда в единицу времени.

Можно рассчитать двумя способами:

1) как отношение абсолютного прироста к уровню:

а) базисный:

;

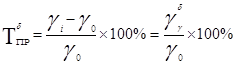б) цепной:

;

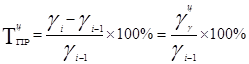2) Как разность между темпом роста и 100%:

.

Между цепными и базисными показателями изменения уровней ряда существует следующая взаимосвязь:

1) сумма цепных абсолютных приростов равна базисному приросту;

2) произведение цепных коэффициентов роста равно базисному;

3) деление рядом стоящих базисных коэффициентов роста друг на друга равно цепным коэффициентам роста.

4. Темп наращивания (пункт роста) рассчитывается делением цепных абсолютных приростов на уровень, принятый за постоянную базу сравнения:

.

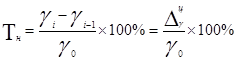5. Абсолютное значение одного процента прироста. Чтобы знать, что скрывается за каждым процентом прироста, рассчитывается абсолютное значение 1% прироста как отношение абсолютного прироста уровня за интервал времени к темпу прироста за тот же промежуток времени:

или .

Иными словами, абсолютное значение 1% прироста в данном периоде- сотая часть достигнутого уровня в предыдущем периоде. В связи с этим расчет абсолютного значения 1% прироста базисным методом не имеет смысла, ибо для каждого периода это будет одна и та же величина- сотая часть уровня базисного периода.

Если систематически растут цепные темпы роста, то ряд развивается относительным ускорением. Относительное ускорение можно определить как разность следующих друг за другом темпов роста или прироста; полученная величина выражается в процентных пунктах (п.п.).

1.2 Средние показатели по рядам динамики.

Для обобщения характеристики динамики исследуемого явления за ряд периодов определяют различного рода средние показатели, среди которых можно выделить:

· средний уровень ряда;

· средний абсолютный прирост;

· средний темп роста и прироста.

Способы расчета среднего уровня различаются и зависят от характеристики ряда.

Рассмотрим две категории средних показателей рядов динамики.

1.Средние показатели изменения уровня ряда: