- оценивание плотностей распределения,

- непосредственное восстановление параметров оптимального решающего правила.

Рассмотрим в отдельности оценивание плотностей распределения.

Оценивание плотностей распределения представляет собой классическую задачу, решаемую в математической статистике. А именно, пусть имеется повторная выборка (то есть, последовательность независимых одинаково распределенных случайных величин) с плотностью распределения p(x). Необходимо построить оценку функции p(x). Известно много методов решения этой задачи, например, метод максимального правдоподобия, байесовские методы оценивания, непараметрические оценки плотностей.

Схема обучения распознавания в таком случае строится следующим образом. Обучающая выборка разбивается на подвыборки, соответствующие отдельным классам. Оцениваются плотности распределений для каждого класса и априорные вероятности классов . Полученные оценки подставляются в байесовское решающее правило (1.2), которое и используется для классификации. Рассмотрим подробно такой метод решения задачи распознавания, как парзеновские оценки плотностей.

2. Непараметрические парзеновские оценки плотност ей

2.1 Основные понятия, определения, теоремы

Методы оценивания, в которых не делается предположений об аналитическом виде неизвестной плотности, называются непараметрическими.

Пусть - повторная выборка с плотностью p(x). Парзеновская оценка плотности p(x) есть функция

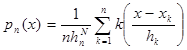, (2.1)

где k(y) – некоторая заданная функция, называемая ядром оценки (2.1), - неотрицательная числовая последовательность.

Если ядро k(y) удовлетворяет условиям

то (2.1) есть плотность распределения.

Докажем следующие теоремы:

Теорема (2.1):

Пусть выполнены условия на ядро k и :

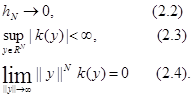
Если функция p(x) непрерывна в точке х, то

геометрический распознавание непараметрический парзеновский

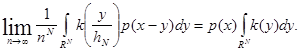
Доказательство.

Рассмотрим величину:

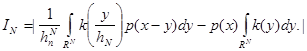
Справедлива формула:

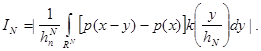
Разобьем здесь область интегрирования на два множества и - произвольное положительное число.

Первое слагаемое не превосходит величины

а второе не превосходит