Курсовая работа: Методы распознавания образов

Многомерные ядра могут быть получены из одномерных следующим образом:

,

где x – вектор с компонентами . Условия (2.4), (2.6) выполнены для последовательностей вида

где а – некоторая константа.

2.2 Исследование парзеновских оценок плотностей на практике

В данном исследовании была поставлена задача смоделировать повторную выборку, соответствующую плотности распределения

() и применить к ней парзеновскую оценку, а также сравнить графически найденную оценку с истинной плотностью.

Работа выполняется в пакете MicrosoftExcel, так как этот пакет один из наиболее пригодных для решения подобных задач.

На интервале [-4;9] с шагом 0,2 построим графическое изображение истинного значения плотности распределения по заданной нам функции при .

Полученный результат представлен на рис. 1:

Рис. 1. График заданной плотности распределения

Для оценивания ее строим повторную (обучающую) выборку, соответствующую данной плотности распределения. В качестве ядра k(y) выберем функцию

.

Проверим, удовлетворяет ли при N=1 функция условиям теорем (2.1) и (2.2).

(a)

где а – некоторая константа,

(b) ,

(c)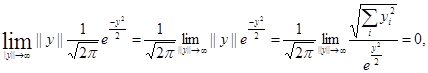

(d) Функция непрерывна во всех точках х,

(e) .

Таким образом, условия теорем выполнены, и оценка является асимптотически несмещенной оценкой величины p(x) (в силу условий (а)-(d)), то есть

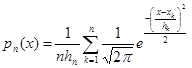
и состоятельной оценкой (в силу условий (а)-(е)), то есть

В зависимости от выбора множителя оценки будут принимать различный вид. Графики сравнения оценки с истинным значением функции при различных представлены на рис. 2-5.