Курсовая работа: Методы распознавания образов

Устремляя n к бесконечности, получаем в силу условий (2.2)-(2.4) получаем:

а так как может быть взято произвольно малым, то это и означает сходимость .

Теорема доказана.

Теорема (2.2).

Пусть х – точка непрерывности плотности p(x) и выполнены условия теоремы (2.1). тогда - асимптотически несмещенная оценка величины p(x), то есть

Если, кроме того

то - состоятельная оценка, то есть

Доказательство.

Соотношение (2.5) непосредственно следует из теоремы (1).

Справедливо равенство

второе слагаемое в правой части стремиться к нулю при .

Введем обозначения:

;

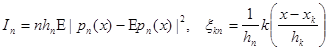тогда

а так как - независимые одинаково распределенные случайные величины, то

При больших n:

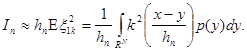
Так как функция удовлетворяет условиям теоремы (2.1), то

Теорема доказана.

При N=1 следующие функции удовлетворяют условиям (2.7)