Курсовая работа: Методы решения задачи о рюкзаке
End ;
Как было сказано ранее, алгоритм динамического программирования для ‘рюкзака’ дает точное решение путем использования дополнительной памяти O(N*MaxW), временная сложность алгоритма так же будет порядка O(N*MaxW).
2.3 Полный перебор
Название метода говорит само за себя. Чтобы получить решение нужно перебрать все возможные варианты загрузки. Здесь мы будем рассматривать такую постановку задачи. В рюкзак загружаются предметы N различных типов (количество предметов каждого типа не ограничено), каждый предмет типа I имеет вес Wi и стоимость Pi , i=(1,2..N). Требуется определить максимальную стоимость груза вес, которого не превышает W. Очевидна простая рекурсивная реализация данного подхода Рис 1.4. Временная сложность данного алгоритма равна O(N!). Алгоритм имеет сложность факториал и может работать лишь с небольшими значениями N. С ростом N, число вариантов очень быстро растет, и задача становится практически неразрешимой методом полного перебора. На рис 1.5 показано дерево перебора, дерево имеет 4 уровня. В каждом кружочке показан вес предмета, корень дерева – нулевой вес, то есть когда рюкзак пуст. Первый предмет можно выбрать четырьмя способами, второй – тремя, третий – двумя, а дальше можем взять только один оставшийся предмет.
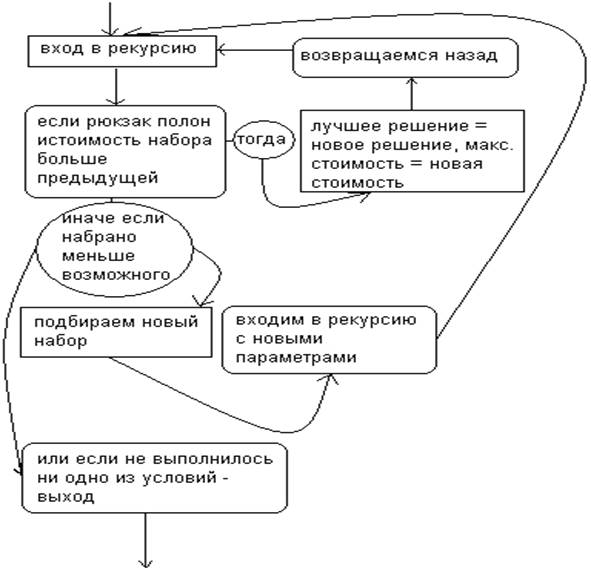
Рис 1.4
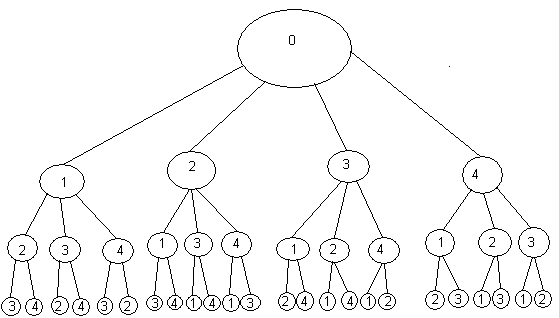
Рис 1.5
N - Количество предметов. Пусть MaxW - объем рюкзака, Pi – стоимость i-го предмета, Wi – вес i-го предмета.
{передаем Nab - номер набранной группы, OstW-вместимость, stoim-цена набранного (еще не набрали нисколько)}
Procedure Search(Nab, OstW, Stoim:integer);
var i:integer;
begin
{здесь OstW-вес который следует набрать из оставшихся. Stoim-стоимость текущего решения}
{Nab - набор предметов если наполнили рюкзаки набрали стоимость больше чем имеется, то считаем это новым решением}
if (Nab > N) and (Stoim > Max) then begin
{найденорешение}
BestP:=NowP;
Max:=Stoim;
End
{иначе если количество взятых <= обьема.
забиваем рюкзак дальше}
else if Nab<=N then
{иначе если набрано меньше чем влазит}
for i:=0 to OstW div W[Nab] do begin
{идем от 0 до ост. места}
NowP[Nab]:=i;
{берем предмет Nab пока есть место в ранце}
Search(Nab+1,OstW-i*W[Nab],Stoim+i*P[Nab]);
{после каждого взятия предмета увеличиваем
стоимость набора и уменьшаем место в рюкзаке
на вес предмета, так же увеличиваем количество
раз взятия предмета}
end;