Курсовая работа: Методы решения задачи о рюкзаке
· Не использует дополнительных ресурсов компьютера.
· Простота реализации.
Минусы ДП – алгоритма:
· Веса предметов целые, если брать вещественные значения, ДП - алгоритм неприменим!
· Использование большого количества оперативной памяти для хранения таблиц промежуточных решений.
· Для больших значений N количества предметов ДП – алгоритм работает O(![]() ).
).
Плюсы ДП – алгоритма:
· Высокая скорость работы по сравнению с другими алгоритмами (для не больших значений N<50).
· Получаем точное решение.
· Имеем оптимальные загрузки рюкзака для всех его весов от 1 до MaxW
На диаграмме 1. показано соотношение времени работы алгоритмов. По вертикальной оси в 1/10000 секунд. По горизонтальной оси в зависимости от количества предметов. Для ДП алгоритма для количества n предметов брался вес w=10*n, так как скорость работы ДП алгоритма зависит от произведения w *n.
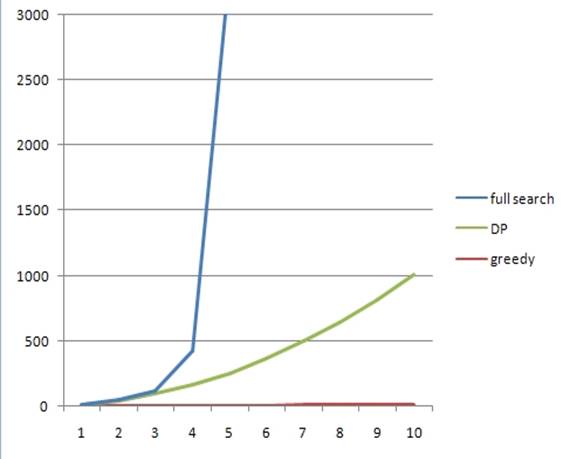
Диаграмма 1
2.7 Модификации задачи
1. Необходимо вывести только максимальную стоимость, набор нас не интересует.
2. В результате работы нужно получить не только максимальную стоимость, но и сам набор.
3. На размер рюкзака несколько ограничений (многомерность задачи).
4. Каждый предмет можно брать только лишь один раз.
5. Предметы можно брать произвольное количество раз.
6. Количество раз помещения предмета в рюкзак фиксировано. Либо для каждого предмета свое, либо для всех предметов одно.
7. Некоторые предметы должны обязательно быть уложены в рюкзак (имеют приоритет).
8. Находить несколько оптимальных решений (одинаковой стоимости, но с разным содержимым).
Заключение
В ходе исследования задачи о рюкзаке были выявлены три основных алгоритма решения. Полный перебор, ДП – программирование, жадный алгоритм. Так же был рассмотрен Метод ветвей и границ, но как сокращение полного перебора. Все методы разделены на две группы. Первая группа – точные методы, сюда входят ДП – алгоритмы, Полный перебор и Метод ветвей и границ. Вторая группа – приближенные методы, к таким методам относится Жадный алгоритм. Выбор использования того или иного метода спорный вопрос, все зависит от постановки задачи, а так же от того, какие цели поставлены. Если требуется найти точное решение, то конечно нужно использовать точные методы, при небольшом наборе входных данных (предметов до 10-20), подойдет перебор или метод ветвей и границ в силу простоты реализации, при больших, следует использовать ДП – алгоритм. Если же точность решения не так важна, или входные данные таковы, что ни один из точных методов не работоспособен, остается применять только приближенные алгоритмы. Но остается возможность комбинирования различных методов для ускорения, или даже применение каких либо “уловок” для конкретного примера. Надеяться же на построение полиномиального алгоритма нет смысла, так как данная задача NP-полна. Безусловно, данная задача очень важна с точки зрения ее приложения в реальной жизни. Не смотря на свою “древность”, рюкзак не только не забывается, наоборот, интерес к нему задаче растет. Оптимальная загрузка транспорта помогает сокращать расходы, получать большую прибыль. Также задача применяется в криптографии и прикладной математике.
Литература
1. Вирт, Н. Алгоритмы и структуры данных [Текст] / Н. Вирт. – Пер. с англ.-М.Мир, 1989.-360 с., ил.
2. Визгунов, Н.П. Динамическое программирование в экономических задачах с применением системы MATLAB [Текст] / Н.П. Визгунов. – Н.Новгород.: ННГУ, 2006. – 48 с.
3. Кузюрин, Н.Н Сложность комбинаторных алгоритмов. Курс лекций [Текст] / Н.Н. Кузюрин, С.А.Фомин. – 2005. – 79 с.
4. Гери, М. Вычислительные машины и труднорешаемые задачи [Текст] / М. Гери, Д. Джонсон. – М.: Мир, 1982 – 416 с.
5. Окулов, С. М - Программирование в алгоритмах [Текст] / С.М. Окулов. – М.: БИНОМ. Лаборатория знаний, 2004. – 341 с.: ил.
6. Окулов, С.М. Информатика в задачах [Текст] / С.М. Окулов, А.А, Пестов, О.А. Пестов. – Киров: Изд-во ВГПУ, 1998. — 343с.
7. Царев, В.А. Проектирование, анализ и программная реализация структур данных и алгоритмов: Учебное пособие [Текст] / В.А. Царев, А.Ф. Дробанов. – Череповец., 2007. – 169 с.
8. Акулич, И.Л Динамическое программирование в примерах и задачах: Учеб. пособие для студентов эконом. спец. вузов [Текст] / И.Л. Акулич. – М.: Высш. шк., 1986. – 319 с., ил.
9. Хаггари, Р. Дискретная математика для программистов [Текст] / Р. Хаггари. – М.: Техносфера, 2003. – 320с.