Курсовая работа: Моделювання оптимального розподілу інвестицій за допомогою динамічного програмування

1) на інструментальне використання базових універсальних програмних засобів (текстових редакторів, СУБД, табличних процесорів, телекомунікаційних пакетів);

2) на комп’ютерне моделювання, що представляє собою:

- обчислювальне (імітаційне) моделювання;

- “візуалізацію явищ і процесів” (графічне моделювання);

- “високі” технології, що розуміють як спеціалізовані прикладні технології, що використають комп’ютер (як правило, у режимі реального часу) у сполученні з вимірювальними апаратурами, датчиками, сенсорами й т.д.

Отже, укрупнена класифікація абстрактних (ідеальних) моделей така:

а) Вербальні (текстові) моделі. Ці моделі використають послідовності пропозицій на формалізованих діалектах природної мови для опису тієї або іншої області дійсності (прикладами такого роду моделей є міліцейський протокол, правила дорожнього руху).

б) Математичні моделі – дуже широкий клас знакових моделей (заснованих на формальних мовах над кінцевими алфавітами), що широко використає ті або інші математичні методи. Наприклад, можна розглянути математичну модель зірки. Ця модель буде являти собою складну систему рівнянь, що описують фізичні процеси, що відбуваються в надрах зірки. Математичною моделлю іншого роду є, наприклад, математичні співвідношення, що дозволяють розрахувати оптимальний (найкращий з економічної точки зору) план роботи якого-небудь підприємства.

в) Інформаційні моделі – клас знакових моделей, що описують інформаційні процеси (виникнення, передачу, перетворення й використання інформації) у системах найрізноманітнішої природи.

Границя між вербальними, математичними й інформаційними моделями може бути проведена досить умовно; цілком можливо вважати інформаційні моделі підкласом математичних моделей. Однак, у рамках інформатики як самостійної науки, відділеної від математики, фізики, лінгвістики й інших наук, виділення інформаційних моделей в окремий клас є доцільним.

Існують й інші підходи до класифікації абстрактних моделей; загальноприйнята точка зору тут ще не встановилася. Зокрема, є тенденція різкого розширення змісту поняття “інформаційна модель”, при якому інформаційне моделювання містить у собі й вербальні, і математичні моделі.

Математична модель виражає істотні риси об’єкта або процесу мовою рівнянь й інших математичних засобів. Власне кажучи, сама математика зобов’язана своїм існуванням тому, що вона намагається відбити, тобто промоделювати, на своїй специфічній мові закономірності навколишнього світу.

Шлях математичного моделювання в наш час набагато більш всеосяжний, ніж моделювання натурного. Величезний поштовх розвитку математичного моделювання дало поява ЕОМ, хоча сам метод зародився одночасно з математикою тисячі років тому.

Математичне моделювання динамічних систем, як таке, аж ніяк не завжди вимагає комп’ютерної підтримки. Кожен фахівець, що професійно займається математичним моделюванням, робить все можливе для аналітичного дослідження моделі. Аналітичні рішення (тобто представлені формулами, що виражають результати дослідження через вихідні дані) звичайно зручніші й інформативніші чисельних. Можливості аналітичних методів рішення складних математичних завдань, однак, дуже обмежені й, як правило, ці методи набагато складніше чисельних. На рисунку 1 представлена процес математичного моделювання з використанням комп’ютерної техніки.

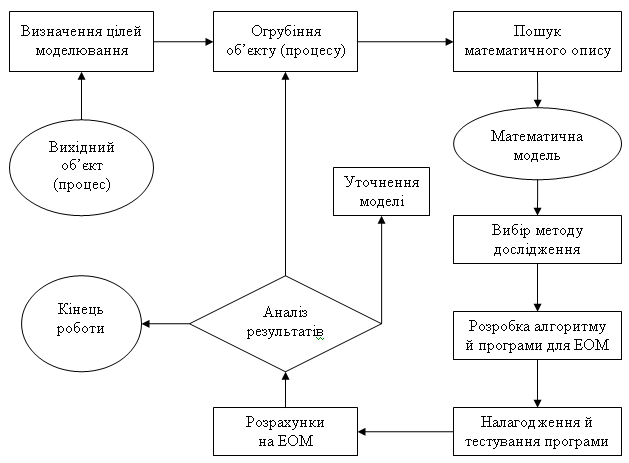
Рисунок 1.1 – Загальна схема процесу комп’ютерного математичного моделювання

Найважливішим етапом моделювання динамічних систем є поділ вхідних параметрів за ступенем важливості впливу їхніх змін на вихідні. Такий процес називається ранжируванням (поділом по рангах). Найчастіше неможливо (та й не потрібно) ураховувати всі фактори, які можуть вплинути на значення величин, що цікавлять, . Від того, наскільки вміло виділені найважливіші фактори, залежить успіх моделювання, швидкість й ефективність досягнення мети. Виділити більш важливі (або значимі) фактори й відсіяти менш важливі може лише фахівець у тій предметній області, до якої відноситься модель.

1.2 Принципи моделювання динамічних систем

інвестиція моделювання динамічний програмування

Розглядаються основні принципи моделювання динамічних систем, у стислій формі відображаючи той достатньо багатий досвід, що накопичений до теперішнього часу в області розробки й використання математичних моделей динамічних систем.

– Принцип інформаційної достатності. При повній відсутності інформації про досліджувану систему побудова її моделі неможлива. При наявності повної інформації її моделювання позбавлене змісту. Існує деякий критичний рівень апріорних відомостей про систему (рівень інформаційної достатності), при досягненні якого може бути побудована її адекватна модель.

– Принцип здійсненності. Створювана модель повинна забезпечувати досягнення поставленої мети дослідження з імовірністю, що істотно відрізняється від нуля, і за кінцевий час. Звичайно задають деяке граничне значення імовірності досягнення цілі моделювання , а також прийнятну границю часу досягнення цієї мети. Модель вважають здійсненною, якщо може бути виконана умова .

– Принцип множинності моделей. Даний принцип, незважаючи на його місцезнаходження у даній класифікації, є ключовим. Мова йде про те, що створювана модель повинна відбивати в першу чергу ті властивості реальної системи (або явища), які впливають на обраний показник ефективності. Відповідно при використанні будь-якої конкретної моделі визнаються лише деякі сторони реальності. Для більш повного її дослідження необхідний ряд моделей, що дозволяють із різних сторін і з різним ступенем детальності відбивати розглянутий процес.

– Принцип агрегування. У більшості випадків складну систему можна представити такою, що складається з агрегатів (підсистем), для адекватного математичного опису яких виявляються придатними деякі стандартні математичні схеми. Принцип агрегування дозволяє, крім того, досить гнучко перебудовувати модель залежно від завдань дослідження.

– Принцип параметризації. У ряді випадків система, що моделюється, має у своєму складі деякі відносно ізольовані підсистеми, що характеризуються певним параметром, у тому числі векторним. Такі підсистеми можна заміняти в моделі відповідними числовими величинами, а не описувати процес їхнього функціонування. При необхідності залежність значень цих величин від ситуації може задаватися у вигляді таблиці, графіка або аналітичного вираження (формули). Принцип параметризації дозволяє скоротити обсяг і тривалість моделювання. Однак треба мати на увазі, що параметризація знижує адекватність моделі [7].

1.3 Моделі і методи прийняття управлінських рішень з урахуванням фактору часу

При прийнятті рішень в практиці управління постає питання про задачу прийняття рішень з урахуванням фактору часу. Задача прийняття рішень спрямована на визначення найкращого (оптимального) або сприятливого способу дій для досягнення однієї або декількох цілей. Під ціллю розуміється в широкому значенні ідеальне уявлення бажаного стану чи результату діяльності. Бажаний стан чи результат для особи, що приймає рішення може означати прибуток фірми, заволодіння долею ринку, подолання конкурентної боротьби, зниження собівартості продукції тощо. Найчастіше у житті трапляється так, що бажаний стан дещо віддалений або взагалі відсутній і той стан який існує в конкретний момент прийнято називати фактичним станом, тобто тим, що не залежить від волі особи, яка приймає рішення (ОПР). Отже, якщо фактичний стан не відповідає бажаному стану, то має місце проблемна ситуація, або проблема, розробка плану подолання якої і складає сутність задачі прийняття рішень.

Проблемна ситуація може виникати за умов коли:

а) функціонування управлінської системи в певний момент часу не забезпечує досягнення бажаних цілей організації;

б) функціонування цієї системи не може забезпечити досягнення цих цілей і в майбутньому;

в) система вимагає докорінних змін поставлених цілей.