Курсовая работа: Нахождение корней уравнения методом Ньютона (ЛИСП-реализация)

Возьмем за начальную точку , тогда

-2.3;

-2.034615;

-2.000579;

-2.0.

Таким образом, корень уравнения

равен -2.

2. Математические и алгоритмические основы решения задачи

2.1 Описание метода

Пусть корень x уравнения отделен на отрезке [a, b], причем и непрерывны и сохраняют определенные знаки при . Если на некотором произвольном шаге n найдено приближенное значение корня

,

то можно уточнить это значение по методу Ньютона. Положим

, (1)

где считаем малой величиной. Применяя формулу Тейлора, получим:

.

Следовательно,

.

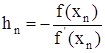Внеся эту поправку в формулу (1), найдем следующее (по порядку) приближение корня

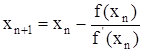
. (2)

Геометрически метод Ньютона эквивалентен замене дуги кривой касательной, проведенной в некоторой точке кривой. В самом деле, положим для определенности, что при и (рисунок 1).

Выберем, например, , для которого . Проведем касательную к кривой в точке B₀ с координатами .

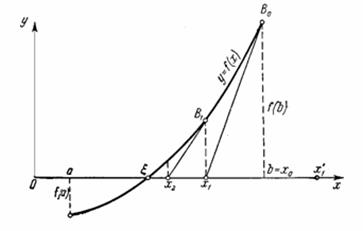
Рисунок 1. Геометрически показан метод Ньютона

В качестве первого приближения корня x возьмем абсциссу точки пересечения касательной с осью Ox. Через точку снова проведем касательную, абсцисса точки пересечения которой даст второе приближение корня x и т.д.

Формулу для уточнения корня можно получить из прямоугольного треугольника , образованного касательной, проведенной в точке B₀ , осью абсцисс и перпендикуляром, восстановленным из точки .

Имеем

.

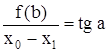Так как угол a образован касательной и осью абсцисс, его тангенс численно равен величине производной, вычисленной в точке, соответствующей абсциссе точки касания, т.е.

.