// ---вывод ребер

cout<<endl<<" Vivod reber maximalnogo vesa: \n ";

a=0;

for (int i=1; i<n; i++)

for (int j=0; j<i; j++)

if (T [i] [j] <max && T [i] [j]! =0) {

L [a] [0] =i+1;

L [a] [1] =j+1;

L [a] [2] =T [i] [j];

a++;

}

for (int i=0; i<kolreb; i++) {

cout<<L [i] [0] <<"-->";

cout<<L [i] [1] <<" = ";

cout<<L [i] [2] <<"\n ";

}

int b=0;

for (int i=0; i<kolreb; i++)

b+=L [i] [2];

cout<<endl <<" Stoimost dereva = "<<b; // вывод стоимости

getch ();

// return 0;

}

// --------------------------------------------------------------

6 . Обзор работы программы

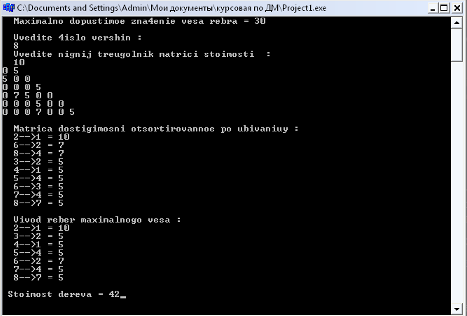
После выполнения программы выводятся ребра максимального веса, и стоимость остовного дерева.

Заключение

В курсовом проекте был разработана программа, реализующая алгоритм Краскала, поиск максимального остовного дерева.

Алгоритм Краскала действительно находит остовный лес максимального веса, поскольку он является частным случаем алгоритма Радо - Эдмондса для графического матроида, где независимые множества - ациклические множества рёбер.

Список использованной литературы

1. Рыбаков Глеб. Минимальные остовные деревья.