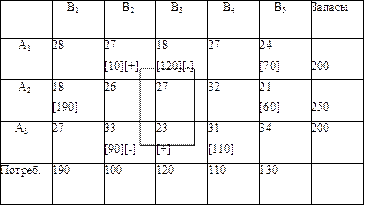Курсовая работа: Нахождение минимальных затрат при распределении товаров среди магазинов методами решения транспо

Проверим необходимое и достаточное условие разрешимости задачи.

Условие баланса соблюдается. Запасы равны потребностям. Построим опорный план транспортной задачи:

B1	B2	B3	B4	B5	Запасы
A1	28 [190]	27 [10]	18	27	24	200
A2	18	26 [90]	27 [120]	32 [40]	21	250
A3	27	33	23	31 [70]	34 [130]	200
Потреб.	190	100	120	110	130

Решение задачи методом северо-западного угла всегда начинается с левого, верхнего тарифа([A₁ ;B₁ ]). Полностью удовлетворяем потребность данного тарифа. Исключаем первый столбец. Дальше смотрим если запасы ещё остались, рассматриваем рядом стоящий тариф ([A₂ ;B₁ ]), если нет, то исключаем и первую верхнею строк. И рассматриваем следующий тариф по аналогичной схеме. В результате получен опорный план, который является допустимым, так как все грузы из баз вывезены, потребность магазинов удовлетворена, а план соответствует системе ограничений транспортной задачи. Подсчитаем число занятых клеток таблицы, их 7, а должно быть m + n - 1 = 7. Следовательно, опорный план является невырожденным.

Подсчитаем затраты на распределение товаров:

F=28*190+27*10+26*90+27*120+32*40+31*70+34*130=19040

Результат: Затраты на распределение товаров между магазинами найденные методом северо-западного угла составят 19040 рублей.

2.3 Нахождение первоначального плана методом наименьшей стоимости

Используя построенную матрицу тарифов, найдём оптимальный опорный план методом наименьшей стоимости.

B1	B2	B3	B4	B5	Запасы
A1	28	27	18	27	24	200
A2	18	26	27	32	21	250
A3	27	33	23	31	34	200
Потреб.	190	100	120	110	130

Проверим необходимое и достаточное условие разрешимости задачи.

Условие баланса соблюдается. Запасы равны потребностям. Построим опорный план транспортной задачи:

B1	B2	B3	B4	B5	Запасы
A1	28	27[10]	18[120]	27	24[70]	200
A2	18 [190]	26	27	32	21[60]	250
A3	27	33 [90]	23	31 [110]	34	200
Потреб.	190	100	120	110	130

Для решения задачи методом наименьшей стоимости сначала из все матрицы тарифов выбираем наименьший тариф ([A₂ ;B₁ ]). Полностью удовлетворяем его потребность. Исключаем из решения столбец в котором он находился. Ищем следующий минимальный тариф ([A₂ ;B₃ ]). Удовлетворяем его потребности. Исключаем из решения столбец в котором он находился. Дальше продолжаем до тех пор, пока все запасы не будут розданы.

В результате получен опорный план, который является допустимым, так как все грузы из баз вывезены, потребность магазинов удовлетворена, а план соответствует системе ограничений транспортной задачи.

Подсчитаем число занятых клеток таблицы, их 7, а должно быть m + n - 1 = 7. Следовательно, опорный план является невырожденным.

Подсчитаем затраты на распределение товаров:

F=27*10+18*120+24*70+18*190+21*60+33*90+31*110=15170

Результат: Затраты на распределение товаров между магазинами найденные методом наименьшей стоимости составят 15170 рублей.

2.4 Метод потенциалов

Для решения транспортной задачи сначала надо найти опорный план методом северо-западного угла и методом наименьшей стоимости, и из них выбрать метод при котором затраты на распределения товаров минимальны.

Для данной задачи минимальным является метод наименьшей стоимости.

Опорный метод этого плана и будем использовать для решения задачи методом потенциалов:

B1	B2	B3	B4	B5	Запасы
A1	28	27[10]	18[120]	27	24[70]	200
A2	18[190]	26	27	32	21[60]	250
A3	27	33[90]	23	31[110]	34	200
Потреб.	190	100	120	110	130

Проверим оптимальность опорного плана. Найдем потенциалы u_i , v_i . по занятым клеткам таблицы, в которых u_i + v_i = c_ij

Для этого построим систему уравнений:

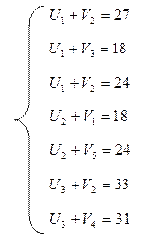
Из этой системы уравнений находим потенциалы , полагая, что u₁ = 0:

v1=0, v2=27, v3=18, v4=25, v5=24, u1=0, u1=-3, u3=6

v1=0	v2=27	v3=18	v4=25	v5=24
u1=0	28	27[10]	18[120]	27	24[70]
u2=-3	18[190]	26	27	32	21[60]
u3=6	27	33[90]	23	31[110]	34

Опорный план не является оптимальным, так как существуют оценки свободных клеток для которых u_i + v_i > c_{ij ,} (3;3): 6 + 18 > 23

Выбираем максимальную оценку свободной клетки (3;3): 23

Для этого в перспективную клетку (3;3) поставим знак "+", а в остальных вершинах многоугольника чередующиеся знаки "-", "+", "-". Цикл приведен в таблице.