Курсовая работа: Нахождение полиноминальной аппроксимации методом наименьших квадратов
Доверительной областью ![]() статистического критерия называется область значений
статистического критерия называется область значений ![]() статистики
статистики ![]() , при которых гипотеза
, при которых гипотеза ![]() принимается.
принимается.
Практическая часть.
Этап 1 (Вычисление оценок ![]() ,
, ![]() неизвестных коэффициентов регрессии
неизвестных коэффициентов регрессии ![]() ,
, ![]() ):
):
![]() ;
;
![]() ;
;
![]() - оценка полезного сигнала (кривая регрессии);
- оценка полезного сигнала (кривая регрессии);
![]() - ошибка;
- ошибка;
Формулируем все ошибки:
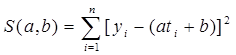 .
.
Находим наименьшую ошибку. Для этого продифференцируем уравнение по a и по b , приравняем к 0, получив систему:
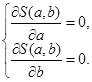 - система нормальных уравнений.
- система нормальных уравнений.
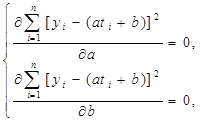
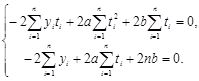
Решаем систему методом Крамера:
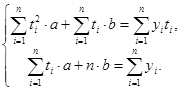
Расчетная схема для оценок ![]() по методу наименьших квадратов.
по методу наименьших квадратов.
| Номер | Y | X | y^2 | X*Y | x^2 | δ^2=(y-at-b)^2 |
| 1 | 13,393 | -2 | 179,37245 | -26,786 | 4 | 84,52154547 |
| 2 | 13,207 | -1,92 | 174,42485 | -25,3574 | 3,6864 | 77,33345969 |
| 3 | 13,477 | -1,84 | 181,62953 | -24,7977 | 3,3856 | 63,01706699 |
| 4 | 11,911 | -1,76 | 141,87192 | -20,9634 | 3,0976 | 79,54344995 |
| 5 | 14,311 | -1,68 | 204,80472 | -24,0425 | 2,8224 | 35,20165139 |
| 6 | 14,979 | -1,6 | 224,37044 | -23,9664 | 2,56 | 21,89755599 |
| 7 | 14,437 | -1,52 | 208,42697 | -21,9442 | 2,3104 | 21,49126227 |
| 8 | 14,957 | -1,44 | 223,71185 | -21,5381 | 2,0736 | 12,46267515 |
| 9 | 13,044 | -1,36 | 170,14594 | -17,7398 | 1,8496 | 23,59662672 |
| 10 | 112,142 | -1,28 | 12575,828 | -143,542 | 1,6384 | 8991,966406 |
| 11 | 12 | -1,2 | 144 | -14,4 | 1,44 | 22,3767305 |
| 12 | 11,496 | -1,12 | 132,15802 | -12,8755 | 1,2544 | 21,61124277 |
| 13 | 12,927 | -1,04 | 167,10733 | -13,4441 | 1,0816 | 6,928339322 |
| 14 | 11,849 | -0,96 | 140,3988 | -11,375 | 0,9216 | 9,762864991 |
| 15 | 11,612 | -0,88 | 134,83854 | -10,2186 | 0,7744 | 7,705858746 |
| 16 | 10,401 | -0,8 | 108,1808 | -8,3208 | 0,64 | 11,56902772 |
| 17 | 8,755 | -0,72 | 76,650025 | -6,3036 | 0,5184 | 19,90687251 |
| 18 | 8,185 | -0,64 | 66,994225 | -5,2384 | 0,4096 | 19,76777254 |
| 19 | 9,681 | -0,56 | 93,721761 | -5,42136 | 0,3136 | 5,590769531 |
| 20 | 9,644 | -0,48 | 93,006736 | -4,62912 | 0,2304 | 3,29736681 |
| 21 | 9,073 | -0,4 | 82,319329 | -3,6292 | 0,16 | 3,244500827 |
| 22 | 8,535 | -0,32 | 72,846225 | -2,7312 | 0,1024 | 3,075233208 |
| 23 | 9,062 | -0,24 | 82,119844 | -2,17488 | 0,0576 | 0,410905071 |
| 24 | 7,602 | -0,16 | 57,790404 | -1,21632 | 0,0256 | 2,296447057 |
| 25 | 9,164 | -0,08 | 83,978896 | -0,73312 | 0,0064 | 0,399692323 |
| 26 | 6,913 | 0 | 47,789569 | 0 | 0 | 1,067444888 |
| 27 | 9,749 | 0,08 | 95,043001 | 0,77992 | 0,0064 | 5,704661232 |
| 28 | 5,543 | 0,16 | 30,724849 | 0,88688 | 0,0256 | 1,517679181 |
| 29 | 5,901 | 0,24 | 34,821801 | 1,41624 | 0,0576 | 0,083131718 |
| 30 | 5,901 | 0,32 | 34,821801 | 1,88832 | 0,1024 | 0,088381223 |
| 31 | 6,76 | 0,4 | 45,6976 | 2,704 | 0,16 | 3,034234095 |
| 32 | 4,593 | 0,48 | 21,095649 | 2,20464 | 0,2304 | 0,025766932 |
| 33 | 6,131 | 0,56 | 37,589161 | 3,43336 | 0,3136 | 5,217278758 |
| 34 | 3,651 | 0,64 | 13,329801 | 2,33664 | 0,4096 | 0,151906494 |
| 35 | 3,796 | 0,72 | 14,409616 | 2,73312 | 0,5184 | 1,255222992 |
| 36 | 3,663 | 0,8 | 13,417569 | 2,9304 | 0,64 | 2,474275069 |
| 37 | 3,068 | 0,88 | 9,412624 | 2,69984 | 0,7744 | 2,444839854 |
| 38 | 3,008 | 0,96 | 9,048064 | 2,88768 | 0,9216 | 4,364814626 |
| 39 | 2,809 | 1,04 | 7,890481 | 2,92136 | 1,0816 | 6,129731157 |
| 40 | 0,333 | 1,12 | 0,110889 | 0,37296 | 1,2544 | 0,342745729 |
| 41 | 1,73 | 1,2 | 2,9929 | 2,076 | 1,44 | 6,59493426 |
| 42 | -0,072 | 1,28 | 0,005184 | -0,09216 | 1,6384 | 1,827027788 |
| 43 | 0,479 | 1,36 | 0,229441 | 0,65144 | 1,8496 | 6,191594234 |
| 44 | -3,18 | 1,44 | 10,1124 | -4,5792 | 2,0736 | 0,34233389 |
| 45 | -2,962 | 1,52 | 8,773444 | -4,50224 | 2,3104 | 0,047752061 |
| 46 | -5,849 | 1,6 | 34,210801 | -9,3584 | 2,56 | 4,338314281 |
| 47 | -6,153 | 1,68 | 37,859409 | -10,337 | 2,8224 | 3,244489064 |
| 48 | -7,911 | 1,76 | 62,583921 | -13,9234 | 3,0976 | 8,842481446 |
| 49 | -10,134 | 1,84 | 102,69796 | -18,6466 | 3,3856 | 21,26146404 |
| 50 | -11,662 | 1,92 | 136,00224 | -22,391 | 3,6864 | 30,84025156 |
| Сумма | 411,949 | -2 | 16631,368 | -504,296 | 66,72 | 9666,40808 |
Подставив найденные суммы в систему, получаем оценки ![]() :
:
![]() =-7,320193878
=-7,320193878
![]() =7,946172245
=7,946172245
Этап 2 (Вычисление оценки ![]() неизвестной дисперсии
неизвестной дисперсии ![]() шумов
шумов ![]() ):
):
![]()
![]()
![]() , где
, где
n – число измерений;
m – число неизвестных параметров.
Этап 3:
По таблице находим квантиль Стьюдента.
| m/a | 0.85 | 0.9 | 0.95 | 0.975 |
| 47 | 1.0480 | 1.2998 | 1.6779 | 2.0117 |
| 48 | 1.0478 | 1.2994 | 1.6772 | 2.0106 |
| 49 | 1.0475 | 1.2991 | 1.6766 | 2.0096 |
| 50 | 1.0473 | 1.2987 | 1.6759 | 2.0086 |
Фрагмент таблицы 1
При λ=0,975 , квантиль Стьюдента 2.0086