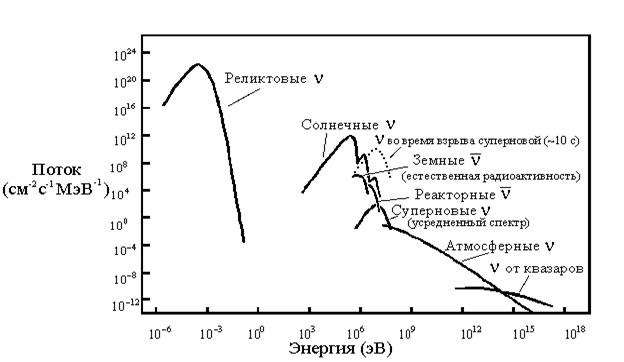
Рисунок 1. Поток нейтрино от различных источников.

Существует три вида, или флейвора, нейтрино: электронное, мюонное и тауонное. До сих пор не ясно отличается ли нейтрино от антинейтрино. Существуют теории в которых они различны. В этом случае говорят о дираковских нейтрино. В других теориях нейтрино и антинейтрино не различимы, и тогда нейтрино называются майорановскими.

Независимо от того являются нейтрино майорновскими или дираковскими, мы не знаем, имеют ли нейтрино массу и магнитный момент. Эксперимент пока обеспечивает верхние пределы. Однако существуют указания на то, что нейтрино имеют массы. Для объяснения некоторых экспериментов выдвигается гипотеза о нейтринных осцилляциях. Осцилляции нейтрино – взаимопревращение различных типов нейтрино. В настоящее время имеется три экспериментальных факта в поддержку нейтринных осцилляций.

1) Поток солнечных оказывается сильно подавленным по сравнению с предсказаниями существующих моделей Солнца.

2) Теоретическое отношение потоков атмосферных мюонных и электронных нейтрино к измеренным экспериментально, находится в противоречии с результатами экспериментов.

3) Изучение распадов движущихся мезонов LSND коллаборацией показывает наличие как так и .

Для существования нейтринных осцилляций необходимо (но не достаточно), чтобы нейтрино имели отличные от нуля массы.

В минимальной стандартной модели не существует правостороннего нейтрино, и значит лептонное число не сохраняется. Таим образом нейтрино не обладает ни майорановской ни дираковской массами. Любое доказательство для ненулевой массы или угла смешивания является доказательством вне рамок стандартной модели. Кроме того, массы и углы смешивания являются фундаментальными параметрами, которые будут объяснены в окончательной теории фермионных масс. Лево-правая модель предсказывает существование нейтринной массы и приводит к смешиванию между состояниями с определенной массой как внутри, так и между нейтринными поколениями.

1. Осцилляции нейтрино.

Осцилляции нейтрино могут быть представлены аналогично более известному примеру прецессии спина в поперечном магнитном поле. Предположим, имеются частицы спина ½, чьи спины поляризованы вдоль z (или “вверх”). Луч проходит через область, где создано магнитное поле в направлении y. Спин “вверх” не является основным состоянием в этом магнитном поле. Из-за этого луч подвергается колебаниям (прецесси). Если рассмотреть луч после прохождения некоторого расстояния, можно обнаружить, что луч является суперпозицией спинов “вверх” и “вниз”.

Можно переформулировать последние утверждение иначе. Мы начинали с луча со спином “вверх”, но после прохождения некоторого расстояния, вероятность найти спин “вверх” в луче меньше единицы. Другими словами, существует истощение спина “вверх”. Осцилляции нейтрино представляют истощение, например солнечных таким же образом, т.е. постулируется, что состояния, которые созданы или наблюдаются, не являются основными состояниями распространения.

1.1. Вакуумные нейтринные осцилляции.

Электронное нейтрино - состояние, возникающие в распаде, где так же рождается позитрон . Мюонное нейтрино - состояние, полученное в распаде вместе с мюоном . Будем называть и состояния флэйвора. Из этого определения не очевидно, что эти состояния флэйвора – физические частицы. Вообще любые из них могут быть суперпозицией из различных физических частиц. Другими словами, состояние полученное в распаде должно иметь некоторую вероятность существования частицы и некоторую вероятность существования частицы . Будем называть эти состояния и , как частицы или физические состояния. Введём следующие обозначения:

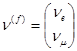
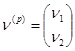( 1.1)

и приняв, что , мы можем написать

( 1.2)

где U – матрица смешивания. Согласно принятому, состояния и ортонормированны, U должна быть унитарной матрицей. В стандартной модели электрослабой физики, все нейтрино безмассовые и следовательно вырождающиеся. В этом случае матрица U не имеет физического смысла. Таким образом, вводя матрицу U, мы полагаем, что нейтрино имеют массу.

Если рассматривать три семейства фермионов, то должна иметь так же состояние и поэтому должна иметь три физических состояния. Тогда матрица смешивания U будет . Ограничемся двумя семействами так, как двух семейств достаточно для объяснения основных теоретических идей, связанных с осцилляциями.

Теперь рассмотрим временную эволюцию лучей нейтрино, которые являются суперпозицией как так и или наоборот и . Эволюционное уравнение будет выглядеть проще на основе :

( 1.3)

H – гамильтониан, диагональный в этом базисе:

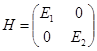( 1.4)

Примем, что , где α=1,2. В этом случае можно написать

( 1.5)

По той же причине мы можем использовать расстояние x, пройденное нейтрино, вместо времени t, в качестве независимой переменной. Разница между t и x введёт высший порядок коррекции в . Так, пространственная эволюция нейтринных лучей регулируется гамильтонианом:

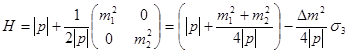( 1.6)

где -диагональная матрица Паули, и

( 1.7)

Далее будем писать уравнение в флэйворном базисе. Это проще сделать используя рав, и равенство :

( 1.8)

которая даёт следующие уравнение движения флэйворного состояния:

( 1.9)

Для двух дираковских нейтрино:

( 1.10)

Поэтому получим гамильтониан в флэйворном базисе в следующем виде:

( 1.11)

Отсюда можно вывести соотношение между диагонализирующим углом и элементами матрицы :

( 1.12)

Так как не зависит от x, мы можем формально интегрировать уравнение движения. Получим:

( 1.13)

Сделаем несколько упрощений. Во-первых, будем писать E вместо . Во-вторых, заметим, что если в существуют слагаемые пропорциональные единичной матрице, то они дают общую фазу для решения. Более того, такие слагаемые не затрагивают угол смешивания, как это видно из уравнения (1.12). Так, как такие слагаемые не относятся к делу, ими можно пренебречь. Тогда получим, что:

( 1.14)

( 1.15)